


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-8-2016
Date: 7-8-2016
Date: 11-8-2016
|
Spherical Void in Dielectric
Suppose there is a spherical void of radius R in an otherwise homogeneous material of dielectric constant ε (see Figure 1.1). At the center of the void is a point dipole p. Solve for the electric field everywhere.
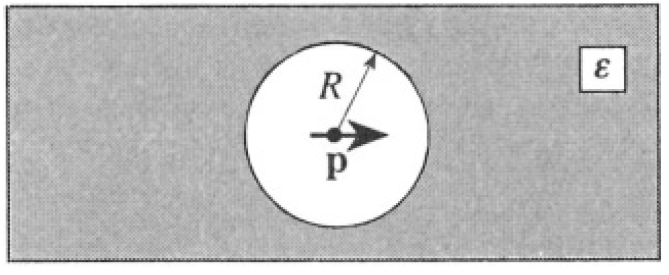
Figure 1.1
SOLUTION
We expect the dipole to induce some charge in the dielectric which would create a constant electric field inside the void, proportional to the dipole moment p. Therefore the field inside is due to the dipole field plus (presumably) a constant field. The field outside is the “screened” dipole field, which goes to zero at infinity. We look for a solution in the form
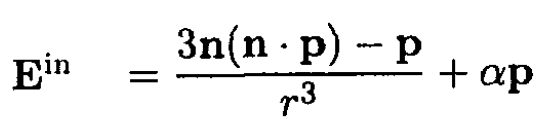 (1)
(1)
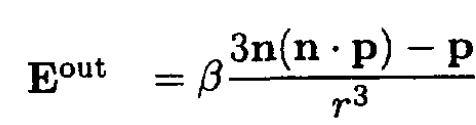 (2)
(2)
where n is normal to the surface of the void (see Figure 1.2). Use the
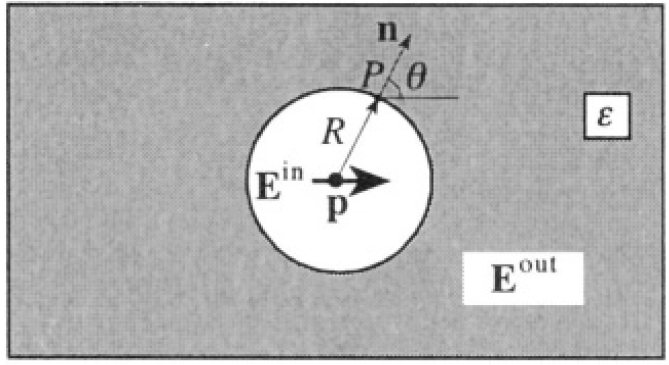
Figure 1.2
boundary conditions to find the coefficients α and β
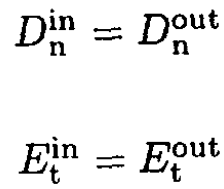
and D = εE, so

Write (1) and (2) at some point P on the surface of the void
 (3)
(3)
 (4)
(4)
where θ is the angle between p and the normal to the surface of the void,
 (5)
(5)
 (6)
(6)
We solve for α and β in (5) and (6):
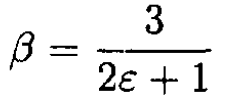 (7)
(7)
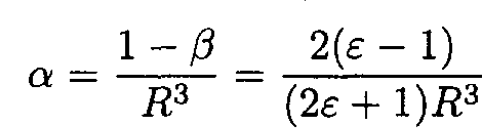 (8)
(8)
and find
 (9)
(9)
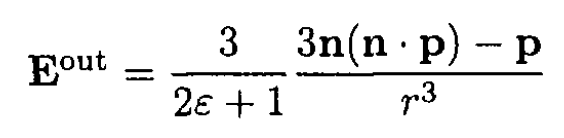 (10)
(10)



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل قائد الفرقة الرابعة الشرطة الاتحادية
|
|
|