


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 11-8-2016
Date: 7-8-2016
Date: 2-8-2016
|
Potential above Half Planes
An infinite conducting plane (the x-z plane in Figure 1.1) is divided by the line z = 0. For x > 0, the potential in the plane is +V0, while for x < 0. the potential is –V0. Evaluate the potential everywhere.
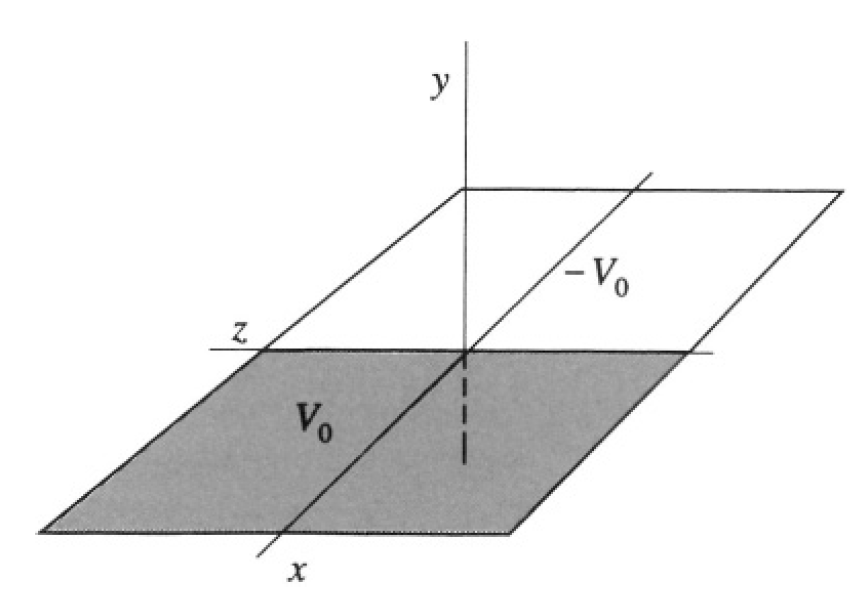
Figure 1.1
SOLUTION
This problem is symmetric for displacements along the z-axis, so we can consider this a two-dimensional problem in the x – y plane, a candidate for the method of conformal mapping. It can be seen that the function ω = ln η (η = x +iy, ω = u + iv) transforms the initial plane so that points at y = 0 for map into the line v = 0, and the points at y = 0 for x < 0 map into the line v = π (see Figure 1.2). In the plane
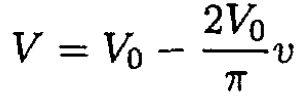
so that at v = 0, V = V0 and at v = π, V = -V0. Again using
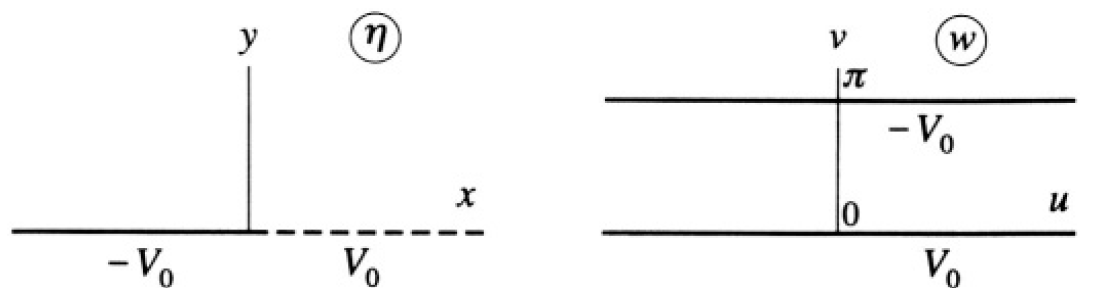
Figure 1.2
η = x – iy = ρeiφ, we obtain
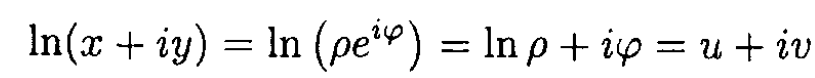
so that
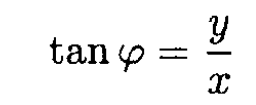
We then have
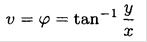
and
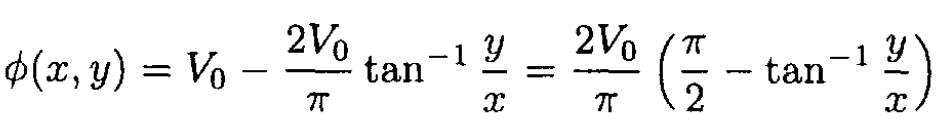
or using
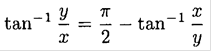
we find
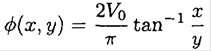
We can check that ϕ (x, y) satisfies the boundary conditions.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|