

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Matchings-Hal,s Theorem and SDRs
المؤلف:
John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff
المصدر:
Combinatorics and Graph Theory, Second Edition
الجزء والصفحة:
104-108
3-8-2016
2458
In this section we consider several classic results concerning matchings. We begin with a few more definitions. Given a graph G and Amatching M ,an M-alternating path is a path in G where the edges alternate between M-edges and non-M-edges .An M-augmenting path is an M-alternating path where both end vertices are M-unsaturated. As an example, consider the graph G and the matching M indicated in Figure 1.1.
An example of an M-alternating path is c, a, d, e, i. An example of an M-augmenting path is j, g, f, a, c, b. The reason for calling such a path “Maugmenting” will become apparent soon.
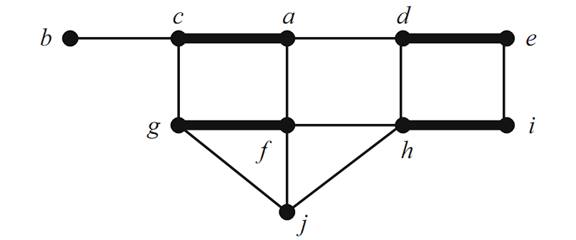
FIGURE 1.1. The graph G and matching M.
The following result is due to Berge [2].
Theorem 1.1 (Berge’s Theorem).
Let M be a matching in a graph G. M is maximum if and only if G contains no M-augmenting paths.
Proof. First, assume that M is a maximum matching, and suppose that P :
v1,v2,...,vk is an M-augmenting path. Due to the alternating nature of M-augmenting paths, it must be that k is even and that the edges v2v3, v4v5, ... , vk−2vk−1 are all edges of M. We also see that the edges v1v2, v3v4, ... , vk−1 vk are not edges of M (Figure 1.2).
But then if we define the set of edgesM1 to be
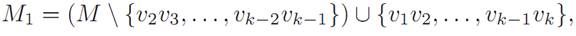
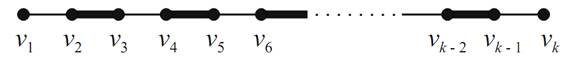
FIGURE 1.2. An M-augmenting path.
then M1 is a matching that contains one more edge than M, a matching that we assumed to be maximum. This is a contradiction, and we can conclude that G contains no M-augmenting paths.
For the converse, assume that G has noM-augmenting paths, and suppose that M/is a matching that is larger than M. Define a subgraph H of G as follows: Let V (H)= V (G) and let E(H) be the set of edges of G that appear in exactly one of M and M/. Now consider some properties of this subgraph H. Since each of the vertices of G lies on at most one edge from M and at most one edge from M/, it must be that the degree (in H) of each vertex of H is at most 2. This implies that each connected component of H is either a single vertex, a path, or a cycle. If a component is a cycle, then it must be an even cycle, since the edges alternate between M-edges and M/-edges. So, since |M/| > |M|, there must be at least one component of H that is a path that begins and ends with edges from M/.
But this path is an M-augmenting path, contradicting our assumption. Therefore, no such matching M/ can exist—implying that M is maximum.
Before we see Hall’s classic matching theorem, we need to define one more term. If G is a bipartite graph with partite sets X and Y , we say that X can be matched into Y if there exists a matching in G that saturates the vertices of X. Consider the two examples in Figure 1.3. In the bipartite graph on the left,
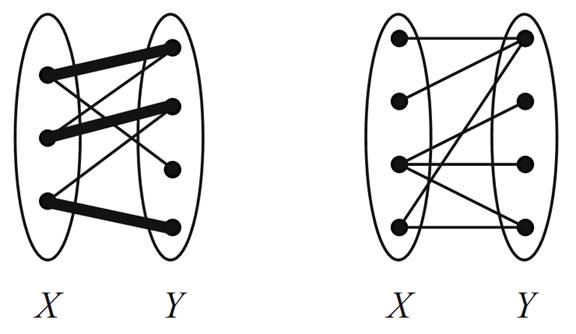
FIGURE 1.3.
we see that X can be matched into Y . In the graph on the right, though, it is impossible to match X into Y. What conditions on a bipartite graph must exist if we want to match one partite set into the other? The answer to this question is found in the following result of Hall [3] (Philip, not Monty).
Recall that the neighborhood of a set of vertices S, denoted by N(S),is the union of the neighborhoods of the vertices of S.
Theorem 1.2 (Hall’s Theorem).
Let G be a bipartite graph with partite sets X and Y . X can be matched into Y if and only if |N(S)|≥|S| for all subsets S of X.
Proof. First suppose that X can be matched into Y ,and let S be some subset of X. Since S itself is also matched into Y , we see immediately that |S|≤|N(S)|
(see Figure 1.4). Now suppose that |N(S)|≥|S| for all subsets S of X, and
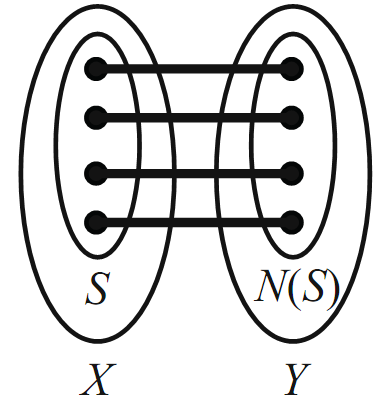
FIGURE 1.4.
let M be a maximum matching. Suppose that u ∈ X is not saturated by M (see Figure 1.5).Define the set A to be the set of vertices of G that can be joined to u
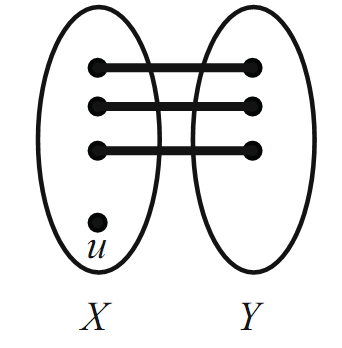
FIGURE 1.5.
by an M-alternating path. Let S = A∩X, and let T = A∩Y (see Figure 1.6). Notice now that Berge’s Theorem implies that every vertex of T is saturated by
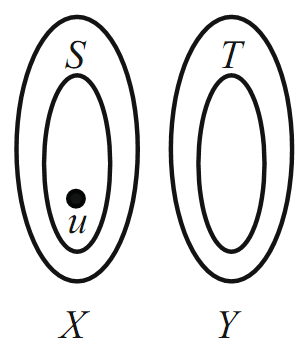
FIGURE 1.6.
M and that u is the only unsaturated vertex of S. That is, every vertex of T is saturated, and every vertex of S {u} is saturated. This implies that |T | = |S|−1.
It follows from Berge’s Theorem and the definition of T that N(S)= T . But then we have that |N(S)| = |S|− 1 < |S|, and this is a contradiction. We conclude that such a vertex u cannot exist in X and that M saturates all of X.
Given some family of sets X,a system of distinct representatives, or SDR ,for the sets in X can be thought of as a “representative” collection of distinct elements from the sets of X. For instance, let S1, S2, S3, S4,and S5 be defined as follows:
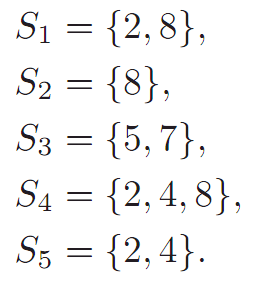
The family X1 = {S1,S2,S3,S4} does have an SDR, namely {2, 8, 7, 4}.The family X2 = {S1,S2,S4,S5} does not have an SDR.
So under what conditions will a finite family of sets have an SDR? We answer this question with the following theorem.
Theorem 1.3.
Let S1, S2, ..., Sk be a collection of finite, nonempty sets. This collection has an SDR if and only if for every t ∈{1,...,k}, the union of any t of these sets contains at least t elements.
Proof. Since each of the sets is finite, then of course S = S1 ∪ S2 ∪···∪ Sk is finite. Let us say that the elements of S are a1, ..., an.
We now construct a bipartite graph with partite sets X = {S1,...,Sk} and Y = {a1,...,an} (Figure 1.7). We place an edge between Si and aj if and only if aj ∈ Si.
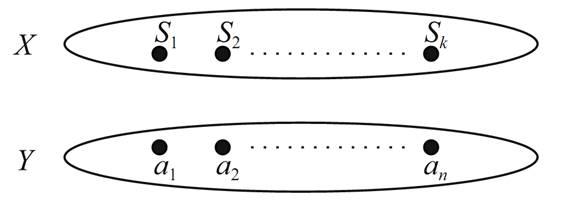
FIGURE 1.7. Constructing a bipartite graph.
Hall’s Theorem now implies that X can be matched into Y if and only if |A|≤|N(A)| for all subsets A of X. In other words, the collection of sets has an SDR if and only if for every t ∈{1,...,k}, the union of any t of these sets contains at least t elements.
________________________________________________________________________________
1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(104-108)
2-C. Berge, Two theorems in graph theory, Proc. Natl. Acad. Sci. USA 43 (1957), 842–844.
3-P. Hall, On representation of subsets, J. London Math. Soc. 10 (1935), 26–30.
4- J. Clark and D. A. Holton, A First Look at Graph Theory, World Scientific, Teaneck, NJ, 1991.
 الاكثر قراءة في نظرية البيان
الاكثر قراءة في نظرية البيان
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















