


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 21-8-2016
Date: 28-7-2016
Date: 9-8-2016
|
Catenary
A flexible cord of uniform density ρ and fixed length l is suspended from two points of equal height (see Figure 1.1). The gravitational acceleration is taken to be a constant g in the negative z direction.
a) Write the expressions for the potential energy U and the length for a given curve z = z(x).
b) Formulate the Euler-Lagrange equations for the curve with minimal potential energy, subject to the condition of fixed length.
c) Show that the solution of the previous equation is given by z = A cosh (x/A) + B where A and B are constants. Calculate U and l for this solution.
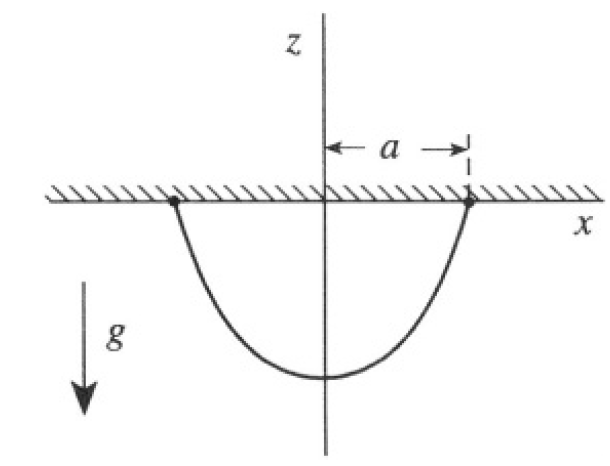
Figure 1.1
Formulae:

SOLUTION
a) Write the expressions for the length and potential energy U (see Figure 1.2) using
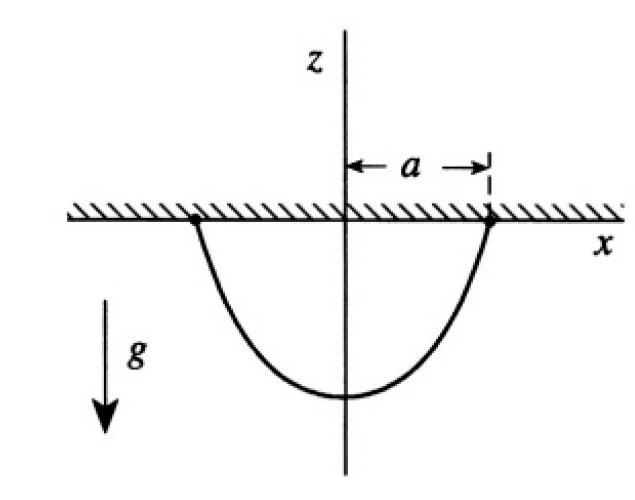
Figure 1.2
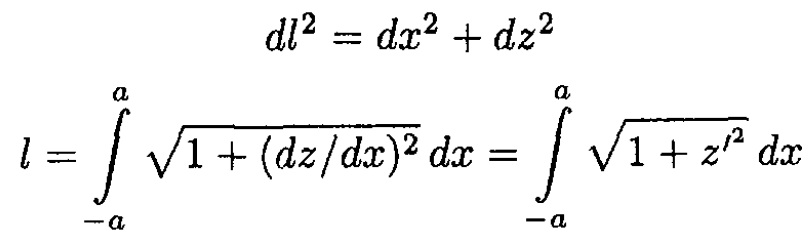 (1)
(1)
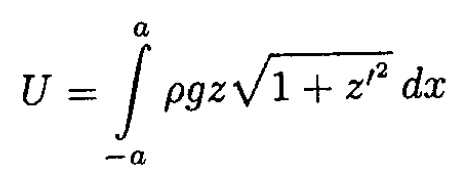 (2)
(2)
b) Here, we are not reproducing the usual Euler–Lagrange equations where we have minimized the action 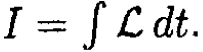 Instead, we look for the minimum of U found in (a), subject to the constraint of constant length l. Utilizing the method of undetermined Lagrange multipliers, λ we may write
Instead, we look for the minimum of U found in (a), subject to the constraint of constant length l. Utilizing the method of undetermined Lagrange multipliers, λ we may write
 (3)
(3)
The coefficient preceding simplifies the calculation. From (3)

where 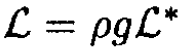
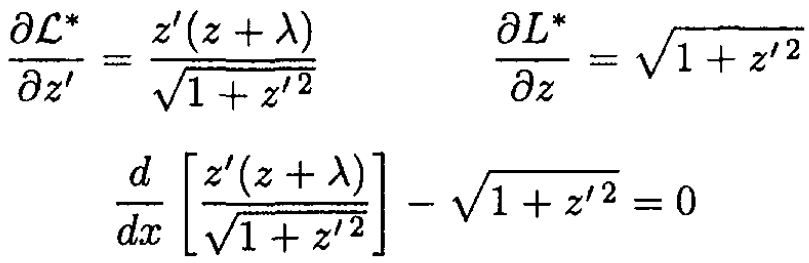 (4)
(4)
Before proceeding to (c), note that in this problem, we may immediately extract a first integral of the motion since  does not depend explicitly on x.
does not depend explicitly on x.
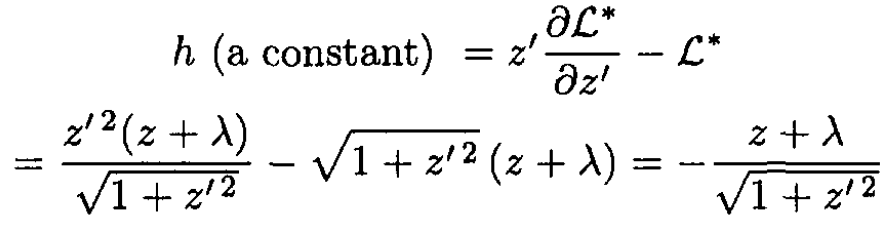 (5)
(5)
c) We may now substitute z = A cosh (x/A) +B into (5), yielding
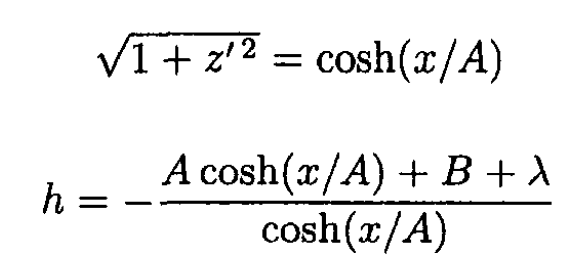 (6)
(6)
h is constant for λ = -B. Calculate from (1):
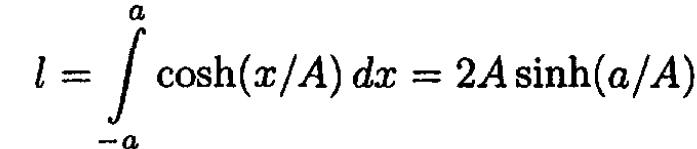 (7)
(7)
Using (2) and (7), find U:
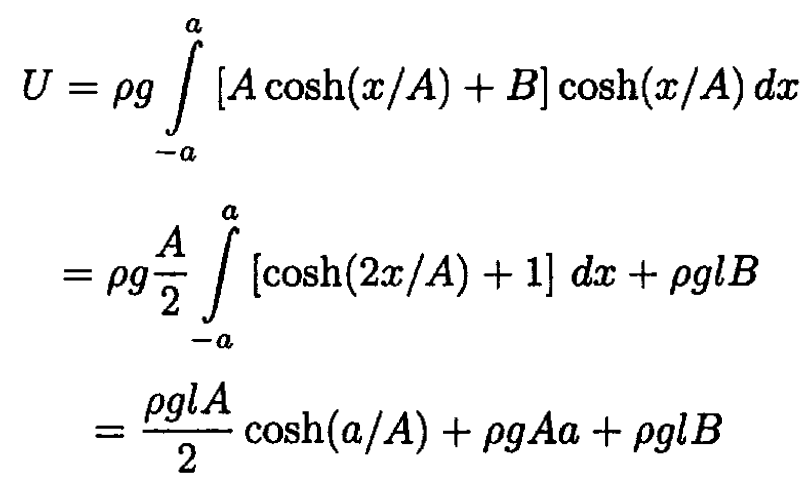 (8)
(8)
Using z(a) = z(-a) = 0, we see that

(8) becomes
 (9)
(9)
From (7), we have
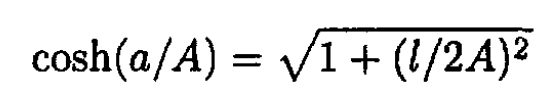
so
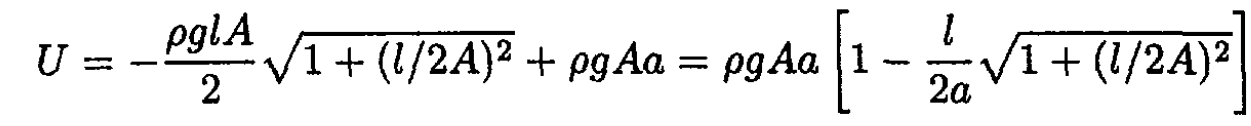



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|