


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-7-2016
Date: 7-7-2016
Date: 8-7-2016
|
Born: 31 July 1777 in Greenock, Scotland
Died: 22 May 1815 in Glasgow, Scotland

William Spence's parents were Sarah Townsend and Ninian Spence, a coppersmith. Sarah and Ninian were married on 15 September 1766 in New Parish Greenock. Their son William was born on the last day of July 1777 and was baptised a few days later on 4 August. He was brought up in Greenock. At the age of four he was sent to the English School (probably run by Hugh Mitchell). During his childhood Spence:-
... was distinguished for his docility and reasonableness, and regulated even his boyish amusements with a degree of gravity only expected in the more comprehensive, but not more interesting transactions of manhood.
John Galt, who was a school friend of Spence and continued the friendship throughout his life, writes [3]:-
When he had just turned his sixth year, the English teacher informed his mother that he should be sent to the grammar school. He was accordingly placed there, and, in the intervals of the classes, received lessons in writing and arithmetic at another school. His progress in Latin was not remarkable; and, incredible as it may now appear, he certainly did not evince any uncommon capacity for arithmetical calculations: but still, such was the originality of his character, that he was undoubtedly considered by his companions as "no vulgar boy."
Spence attended a school in Greenock run by a Mr McGregor "who is described as an excellent teacher, but of wayward temper; and was by him instructed in penmanship and arithmetic, mathematics and the French language." At the age of twelve his school friends were impressed by his ability to caste and bore brass cannon and make gunpowder. In the summer, together with his friends, Spence went fishing or looking for birds' nests. As he grew up Spence turned from reading adventure stories to reading biography and history.
After leaving school, Spence went to Glasgow where he lodged with Mr Struthers, a friend of his father, while he learnt the skills of being a manufacturer. Struthers was a remarkable man who [3]:-
... possessed singular attainments in the languages, and a most profound knowledge of mathematics, accompanied with the most amiable dispositions and a delightful simplicity of character. He was, indeed, in many respects, an extraordinary man. The hours of business were faithfully devoted to thecounting house, and in the evenings, to a late hour, spent in literary and scientific studies.
Eventually Spence gave up learning business skills and devoted himself entirely to the study of science. He continued to live with Struthers until he died in 1797 when he returned to Greenock to live with his mother. By this time his father had also died. At this time he started up a literary society. Galt write in his autobiography [1]:-
... some half dozen or fewer of my companions formed a monthly society, at the instigation of William Spence. We read all sorts of essays about every sort of subject, from the "cedar tree that is on Lebanon to the hyssop that springeth out of the wall", and afterwards discussed philosophical topics, and then had a supper. But we were not so wise when we broke up, which was after midnight, as when the sederunt commenced at seven o'clock. I was the youngest member, and certainly not the best writer; both Spence and Park were superior; but it is curious to observe how early innate character begins to manifest itself. The essays of William Spence were very astronomical, we thought them profound; they were all about planets and comets, the cosmogony of the earth, the infinite divisibility of matter, and the boundless of nature, premundane space; any thing of this world was too gross to enter into his speculative theories.
The Society continued its monthly meetings until the spring of 1804 but still met after that on occasions when members happened to be together. In 1805, in the company of his school friend James Park, Spence visited many places in England, spending some time with Galt, who was at that time living in London. In 1808 Spence was again in London, and during the several months that he lived there, he published An Essay on the various Orders of logarithmic Transcendents; with an Inquiry into their Applications to the Integral Calculus, and the Summation of Series. This work, published by John Murray and Archibald Constable, London and Edinburgh, in 1809 showed him as one of the first British mathematicians to be familiar with the work of Lagrange and Arbogast. On page 63 of the work is a table of the values of the function C-1(x), x = 1 to 100, which is apparently the first table of tan-1x. Spence gave the results to nine decimal places and we note that he did not round off his tables. There are a few errors. For example x = 61 should be 1.554404352 where Spence gives 1.544404352 - clearly a typographical error rather than a calculating error. L C Maximon, in [5], also looks at Spence's contributions:-
The integral
L2(x) = -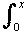 loge(1 - t)/t dt
loge(1 - t)/t dt
has an extensive history that long predates it being named and being referred to as the dilogarithm. ... the first comprehensive detailed study of the function is the essay of Spence (1809), which was generally not referenced on the continent for several decades. (This work was, along with other manuscripts left by Spence, re-edited by John Herschel.) Spence (1820) defines various orders of logarithmic transcendents ...
Spence published his last work "Outlines of a theory of algebraical equations: deduced from the principles of Harriot, and extended to the fluxional or differential calculus" in 1814. It is 90 pages long, cost 15s, but only 80 copies were printed. It is clear that Spence must have read Lagrange's 1770 paper Réflexions sur la résolution algébrique des équations for he tries to make a systematic approach to solving equations of degree 2, 3 and 4 using symmetrical functions of the roots as does Lagrange. This makes it sound as if Spence follows Lagrange rather closely but this is certainly not the case for he gives his own approach to solving these equations. Of course he has no success when he tries to generalise his approach to solving fifth degree equations. James Cockle makes a detailed study of this work by Spence in [2]. In the same year of 1814 Spence went with his sister to London where he married an English lady who he had been engaged to marry for some time. The couple intended to live in London but, after some time, made a visit to Scotland accompanied by Spence's sister. After spending a while in Greenock, they set out to travel to Edinburgh as the first leg of their journey back to England. However Spence was taken ill at Glasgow, and died in the inn in which they had put up for the night.
After Spence died, John Herschel edited Mathematical Essays by the late William Spence which was published by Oliver and Boyd in Edinburgh in 1819. The book, which cost £1 16s, was reviewed in [4]:-
On the appearance of the first of these Essays on the Theory of the various Orders of Logarithmic Transcendents in 1809, its merits were universally acknowledged to entitle the author to hold a high rank among mathematicians. It is to be regretted that a premature death carried him off at a time when he was making such a rapid progress in the cultivation of the sciences. Of these tracts, the first only was intended by the author to meet the public eye in its present shape, though a few copies of another of them, demominated 'Outlines of a Theory of Algebraical Equations', had been printed and distributed among the author's friends. The others were selected from Mr Spence's papers by the editor, J F W Herschel, Esq., who was preeminently qualified to judge the respective merits of the several pieces. These papers clearly prove, that Mr Spence possessed both genius and industry in a high degree, and a force of intellect of a very superior kind. Notwithstanding the disadvantage attending some of these essays, in common with other posthumous works, we warmly recommend them to the attention of the British student, as models of analytic papers of uncommon excellence. They will inspire him with a taste for pure analysis, which, when properly directed, in the present state of the sciences, is the most certain method of arriving at distinction.
Finally we should record Spence's musical abilities. Galt writes [3]:-
In music he was not only a scientific harmonist and a pleasing composer, but he performed on the flute with admirable sweetness and skill. He wrote respectable verses, and had a fine tenor voice, which enabled him to sing pathetic airs, especially of his own composition, with much taste and effect.
Galt also writes in his autobiography [1] of Spence's musical abilities:-
Spence, besides being a most delicious performer was a considerable composer, and made beautiful sonatas, which had as much character as the compositions of Frederick the Great, King of Prussia. I too was a composer, but never got in practice beyond playing duets with Spence.
In [3] Galt gives this tribute to Spence:-
In general knowledge, I do not scruple to say, that in the circle of an acquaintance that embraces many of the most accomplished characters of the age, I have met with no one who, with so much information, united the same colloquial powers of unfolding what he knew. ... There was no subject of which he did not possess a liberal portion of information; in several he was profoundly versed; and with an aptitude that often surprised by its alacrity, he could show himself acquainted with the outlines of all.
A few years after his death, a Marble Tablet bearing an inscription written by Galt, was erected to Spence's memory by several of his friends in the Middle Parish Church in Greenock. The Spence library in Greenock was founded by Spence's widow and contains his books.
Books:
Articles:



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|