


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-05-27
التاريخ: 13-2-2017
التاريخ: 21-9-2020
التاريخ: 2023-04-19
|
انتقال الحرارة والحرارتان النوعيتان للغازات المثالية
تعتمد كمية الحرارة المنتقلة إلى الغاز أو منه ، كالشغل تماماً، على تفاصيل العملية المستخدمة. (ولهذا فإن Q ليست دالة حالة للنظام ). وهناك نوعان من العمليات التي يمكن فيهما حساب الانتقال الحراري مباشرة بمنتهى السهولة وهما: العمليات ثابتة الحجم والعمليات ثابتة الضغط .
العمليات ثابتة الحجم
عندما تضاف الحرارة إلى غاز مع حفظ حجمه ثابتاً يكون الشغل المبذول صفراً (لأن V = 0Δ) ويخبرنا القانون الأول للديناميكا الحرارة أن الحرارة المضافة في هذه الحالة تستهلك في زيادة الطاقة الحرارية:
(1) Q = ΔU (عند ثبوت الحجم)
أن العلاقة بين ΔU و ΔT في حالة الغازات أحادية الذرة تكون على الصورة ΔU = ½ nRΔT وعليه، يمكننا تمثيل العلاقة بين الحرارة المنتقلة إلى الغاز Q والتغير الناتج في درجة حرارته ΔT بالمعادلة:
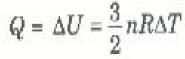
حتى هذه النقطة لم تتعرف إلى على كمية واحدة تربط بين كمية الحرارة Q والتغير الناتج في درجة الحرارة TΔ لكمية معينة من المادة ، وهذه الكمية هي الحرارة النوعية للمادة c = Q/m ΔT، حيث m كتلة العينة. ولكن كمية المادة تقاس عادة في حالة الغازات بالمولات. ومن ثم يمكننا تعريف الحرارة النوعية الجزيئية (او المولارية) C كالتالي:
(2) 
حيث n عدد الملات من الغاز. وحيث ان هذه النسبة تعتمد على نوع عملية الانتقال الحراري، علينا تمييز C يرمز مناسب يشير إلى العملية التي تتحدث عنها. ولذلك فإننا سنستخدم الرمز Cv في حالة العمليات ثابتة الحجم.
نجد أن3/2 nRΔT Q =، وبالتعويض من هذه العلاقة الأخيرة في المعادلة (2) سنحصل على العلاقة البسيطة الآتية:

أما في حالة الجزيئات الاكثر تعقيداً فإن نفس الطريقة تعطينا النتيجة العامة الآتية:

حيث K عدد صحيح.
العمليات ثابتة الضغط
أن W = P ΔV في العملية ثابتة الضغط، وبناء على ذلك يمكن كتابة القانون الأول في هذه الحالة على الصورة:
( 3أ) 
وعندما يكون P ثابتاً فإن قانون الغاز المثالي يعطينا:

وعليه فإن:
( 3ب) 
أنCV ، تعرف الحرارة النوعية الجزيئية عند ثبوت الضغط CP كالتالي:

وحيث أن هذه النتيجة لا تعتمد على نوع الغاز، إذن:

ليس من الغريب أن تكون CP أكبر دائماً من CV. فعند ثبوت يستهلك بعض الحرارة في بذل الشغل الخارجي، ويستهلك الجزء الباقي في زيادة الطاقة الداخلية، أي في رفع درجة الحرارة. إذن، كلما كانت الحرارة النوعية كبيرة، كلما قل التغير في درجة الحرارة لنفس كمية الحرارة المنتقلة.
يرمز للنسبة بين الحرارتين النوعيتين في هاتين العمليتين بالرمز γ، أي أن :
(4) 
الجدول (1) : الحرارة النوعية الجزيئية والكتلية للغازات
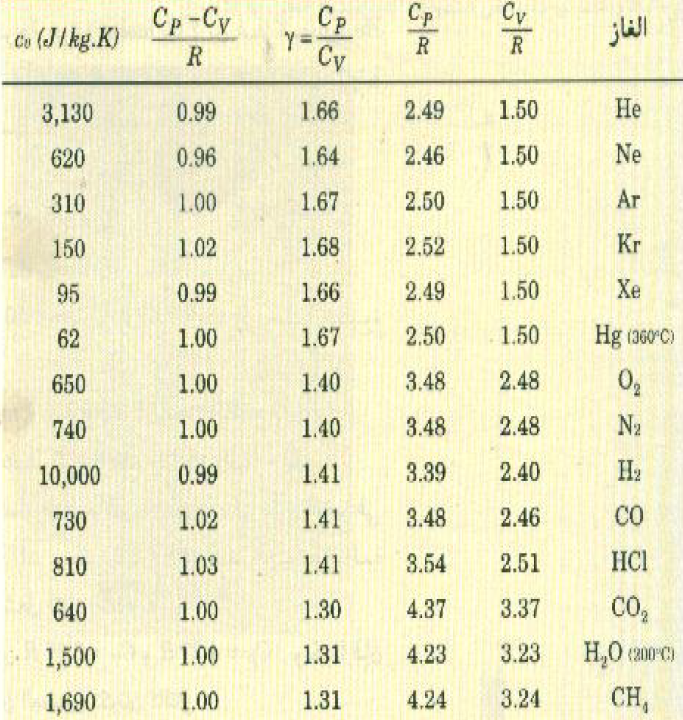
عند درجة 15oC لجميع الغازات ما لم ينص على غير ذلك.
يمثل الجدول ((1 القيم المقاسة عملياً للحرارتين النوعيتين CP و CV والنسبة بينمها Y لعدد من الغازات. لاحظ أن γ = 1.67 للغازات أحادية الذرة، كذلك فإن قيم γ للغازات الأخرى يمكن استخدامها لحساب قيمة K لكل غاز ، إذ أن معادلاتنا السابقة تبين أن (K + 2)/K = γ ففي حالة الغازات ثنائية الذرة يلاحظ من الجدول أن 1.40= 7/5=γ، وهذا يعني أن K = 5. ام بالنسبة للجزيئات المركبة فإن=1.3=4/3γ. وهذه القيمة بالنسبة y تناظر K = 6. نستنتج من ذلك إذن أن التجربة تؤيده ما توقعناه سابقاً بأن k عدد صحيح.
وكاختيار آخر لصحة المعادلات السابق اشتقاقها للحرارتين النوعيتين للغازات يمكننا استخدام العلاقة الآتية:
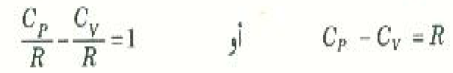
وبالرجوع إلى العمود قبل الأخير في الجدول ((1 سنجد أن هذا صحيح لجميع الغازات.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
العتبة العباسية المقدسة تطلق النسخة الحادية عشرة من مسابقة الجود العالمية للقصيدة العمودية
|
|
|