


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-2-2016
Date: 27-2-2016
Date: 27-2-2016
|
Geometry is one of the oldest crafts – it literally means earth [geo] measuring [metry]. In ordinary geometry there are continuous lines and solid shapes to investigate, both of which can be thought of as being composed of points ‘next to’ each other. Discrete mathematics deals with whole numbers as opposed to the continuous real numbers. Discrete geometry can involve a finite number of points and lines or lattices of points – the continuous is replaced by the isolated.
A lattice or grid is typically the set of points whose coordinates are whole numbers. This geometry poses interesting problems and has applications in such disparate areas as coding theory and the design of scientific experiments.


The lattice points of the x/y axes
Let’s look at a lighthouse throwing out a beam of light. Imagine the light ray starts at the origin O and sweeps between the horizontal and the vertical. We can ask which rays hit which lattice points (which might be boats tied up in the harbour in a rather uniform arrangement).
The equation of the ray through the origin is y = mx. This is the equation of a straight line passing through the origin with gradient m. If the ray is y = 2x then it will hit the point with coordinates x = 1 and y = 2 because these values satisfy the equation. If the ray hits a lattice point with x = a and y = b the gradient m is the fraction b/a. Consequently if m is not a genuine fraction (it may be √2, for example) the light ray will miss all the lattice points.
The light ray y = 2x hits the point A with coordinates x = 1 and y = 2 but it will not strike the point B with coordinates x = 2 and y = 4 and all other points ‘behind’ A (such as C, with coordinates x = 3 and y = 6, and D with x = 4 and y = 8) will be obscured. We could imagine ourselves at the origin identifying the points that can be seen from there, and those that are obscured.
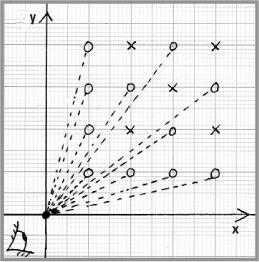
 The points O ‘visible’ from the origin, and the obscured points ×
The points O ‘visible’ from the origin, and the obscured points ×
We can show that those points with coordinates with x = a and x = b which can be seen are those that are relatively prime to each other. These are points with coordinates, such as x = 2 and y = 3, where no number other than 1 divides both x and y. The points behind this one will be multiples, such as x = 4 and y = 6, or x = 6 and y = 9, and so on.
Pick’s theorem
The Austrian mathematician Georg Pick has two claims to fame. One is that he was a close friend of Albert Einstein and proved instrumental in bringing the young scientist to the German University in Prague in 1911. The other is that he wrote a short paper, published in 1899, on ‘reticular’ geometry. From a lifelong work covering a wide range of topics he is remembered for the captivating Pick’s theorem – and what a theorem it is!
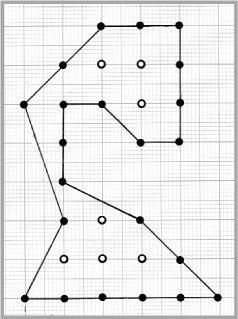
 A many-sided or polygonal shape
A many-sided or polygonal shape
Pick’s theorem gives a means for computing the area enclosed by a many-sided (or polygonal) shape formed by joining up points whose coordinates are whole numbers. This is pinball mathematics.
To find the area of the shape we shall have to count the number of points • on the boundary and the number of interior points o. In our example, the number of points on the boundary is b = 22 and the number of interior points is c = 7. This is all we need to use Pick’s theorem:
area = b/2 + c – 1
From this formula, the area is 22/2 + 7 – 1 = 17. The area is 17 square units. It is as simple as that. Pick’s theorem can be applied to any shape which joins discrete points with whole number coordinates, the only condition being that the boundary does not cross itself.

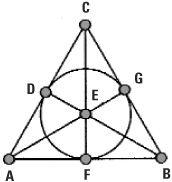
The Fano plane
The Fano plane
The Fano plane geometry was discovered at about the same time as Pick’s formula, but has nothing to do with measuring anything at all. Named after the Italian mathematician Gino Fano, who pioneered the study of finite geometry, the Fano plane is the simplest example of a ‘projective’ geometry. It has only seven points and seven lines.
The seven points are labelled A, B, C, D, E, F and G. It is easy to pick out six of the seven lines but where is the seventh? The properties of the geometry and the way the diagram is constructed make it necessary to treat the seventh line as DFG – the circle passing through D, F and G. This is no problem since lines in discrete geometry do not have to be ‘straight’ in the conventional sense.
This little geometry has many properties, for example:
• every pair of points determines one line passing through both,
• every pair of lines determines one point lying on both.
These two properties illustrate the remarkable duality which occurs in geometries of this kind. The second property is just the first with the words ‘point’ and ‘line’ swapped over, and likewise the first is just the second with the same swaps.
If, in any true statement, we swap the two words and make small adjustments to correct the language, we get another true statement. Projective geometry is very symmetrical. Not so Euclidean geometry. In Euclidean geometry there are parallel lines, that is pairs of lines which never meet. We can quite happily speak of the concept of parallelism in Euclidean geometry. This is not possible in projective geometry. In projective geometry all pairs of lines meet in a point. For mathematicians this means Euclidean geometry is an inferior sort of geometry.

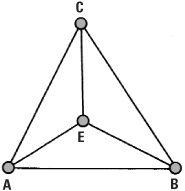
The Fano plane made Euclidean
If we remove one line and its points from the Fano plane we are once more back in the realm of unsymmetrical Euclidean geometry and the existence of parallel lines. Suppose we remove the ‘circular’ line DFG to give a Euclidean diagram.
With one line fewer there are now six lines: AB, AC, AE, BC, BE and CE. There are now pairs of lines which are ‘parallel’, namely AB and CE, AC and BE, and BC and AE. Lines are parallel in this sense if they have no points in common – like the lines AB and CE.


The Fano plane occupies an iconic position in mathematics because of its connection to so many ideas and applications. It is one key to Thomas Kirkman’s schoolgirl problem . In the theory of designing experiments the Fano plane appears as a protean example, a Steiner Triple System (STS). Given a finite number of n objects an STS is a way of dividing them into blocks of three so that every pair taken from the n objects is in exactly one block. Given the seven objects A, B, C, D, E, F and G the blocks in the STS correspond to the lines of the Fano plane.

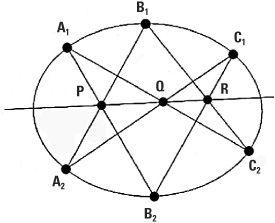
Pascal’s theorem
A pair of theorems
Pascal’s theorem and Brianchon’s theorem lie on the boundary between continuous and discrete geometry. They are different but related to each other. Pascal’s theorem was discovered by Blaise Pascal in 1639 when he was only 16 years old. Let’s take a stretched out circle called an ellipse and mark six points along it that we’ll call A1, B1 and C1 and A2, B2 and C2. We’ll call P the point where the line A1B2 intersects A2B1; Q the point where the line A1C2 intersects A2C1; and R the point where the line B1C2 intersects B2C1. The theorem states that the points P, Q and R all lie on a single straight line.
Pascal’s theorem is true whatever the positions of the different points around the ellipse. In fact, we could substitute a different conic in place of the ellipse, such as hyperbola, circle, parabola or even a pair of straight lines (in which case the configuration is referred to as ‘cat’s cradle’) and the theorem would still be true.

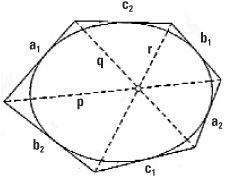
Brianchon’s theorem
Brianchon’s theorem was discovered much later by the French mathematician and chemist Charles-Julien Brianchon. Let’s draw six tangents that we’ll call the lines a1, b1 and c1 and a2, b2 and c2, touching the circumference of an ellipse. Next we can define three diagonals, the lines p, q and r, by the meeting of lines, so that: p is the line between the points where a1 meets b2 and where a2 meets b1; q is the line between the points where a1 meets c2 and a2 meets c1; and r is the line between the points where b1 meets c2 and b2 meets c1. Brianchons’s theorem states that lines p, q and r meet at a point.
These two theorems are dual to each other, and it is another instance of the theorems of projective geometry occurring in pairs.
the condensed idea
Individual points of interest





|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|