An algorithm is a step-by-step procedure to calculate a result. We shall first introduce an algorithm, called the brute force algorithm, to use in those cases where a complete search is feasible. The method involves constructing a tree, called a search tree. Search trees are much the same as the tree diagrams we introduced in (Probability).

Suppose we want to find all Hamilton circuits in a graph G. We construct a tree,  which we shall call T.

First, select any vertex of G as a starting point; call it V say. Construct the first vertex (called the root) of the search tree; label it with V. For every edge of G that contains V, draw an edge of the tree starting at V (called a branch) and label it with the corresponding vertex of G.

To illustrate this, look at the example G shown on the left of Fig. 1.1. Let us start at vertex A. In the graph there are three vertices joined to A, namely B, C and D. So we start three branches, and label them as shown in the right-hand side of figure.

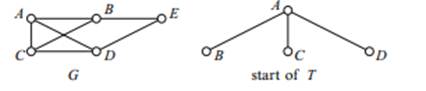
 Fig. 1.1 The brute-force algorithm, step 1

From each new vertex, draw an edge of the tree corresponding to each edge of G that could be an edge of the Hamilton cycle: it must not duplicate an edge of G or complete a cycle in G that misses some vertices. In the example, a branch will go from B to vertices labeledC and E, but not to A (duplication of edge AB) or D (there is no edge in BD in G). Similarly there are two branches from each of C and D. The result is shown in Fig. 1.2.

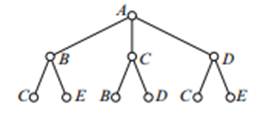
Fig. 1.2 The brute-force algorithm, step 2

Continue in this way from each new vertex of the tree. For example, the path A,B,E can extend only to D, because B would be a repeated edge and E is not connected to A or C. The path A,C,D can extend only to E, because if you try to extend it to C you would repeat the edgeCD, and extending to A would form a cycle of length 3, not big enough for a Hamilton cycle.

As we go on, some of the branches cannot be continued. After A,B,C,D,E there is no possible continuation, because EA is not an edge of G. Others, like A,C,B,E,D,A can be completed: the branch contains every vertex of G and finishes back at A—not a small circuit, because all the vertices are present. The final tree appears in Fig. 1.3.

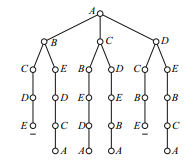
Fig. 1.3 The brute-force algorithm, final result

When the process is finished, the completed branches are the Hamilton cycles.

Each cycle will occur twice, once in each direction. So the example has two Hamilton cycles: ABEDCA and ACBEDA.

As we observed, a complete search is not practical in large cases, especially where the graph is nearly complete. For this reason, fast methods of reaching a  “good solution” have been developed. Although they are not guaranteed to give the optimal answer, these approximation algorithms often give a route that is significantly cheaper than the average. We shall look at two of these.

The nearest-neighbor method works as follows. Starting at some vertex x, one first chooses the edge incident with x whose cost is least. Say that edge is xy. Then an edge incident with y is chosen in accordance with the following rule: if y is the vertex most recently reached, then eliminate from consideration all edges incident with y that lead to vertices that have already been chosen (including x), and then select an edge of minimum cost from among those remaining. This rule is followed until every vertex has been chosen. The cycle is completed by going from the last vertex chosen back to the starting position x. This algorithm produces a cycle in the complete graph, but not necessarily the cheapest one, and different solutions may come from different choices of initial vertex x.

The sorted-edges method does not depend on the choice of an initial vertex. One first produces a list of all the edges in ascending order of cost. At each stage, the cheapest edge is chosen with the restriction that no vertex can have degree 3 among the chosen edges, and the collection of edges contains no cycle of length less than v, the number of vertices in the graph. This method always produces a cycle, and it can be traversed in either direction.

Sample Problem 1.1 Suppose the costs of travel between St. Louis, Nashville,  Evansville, and Memphis are as shown in dollars on the left in Fig. 1.4. You wish to visit all four cities, returning to your starting point. What routes do the two algorithms recommend?

Fig. 1.4 A Traveling Salesman Problem example

Solution. The nearest-neighbor algorithm, applied starting from Evansville,  starts by selecting the edge EM, because it has the least cost of the three edges incident with E. The next edge must have M as an endpoint, and ME is not allowed (one cannot return to E, it has already been used), so the cheaper of the remaining edges is chosen, namely MN. The cheapest edge originating at N is NE, with cost $220, but inclusion of this edge would lead back to E, a vertex that has already been visited, so NE is not allowed, and similarly NM is not available.

It follows that NS must be chosen. So the algorithm finds route EMNSE, with cost $1040.

A different result is achieved if one starts at Nashville. Then the first edge selected is NE, with cost $220. The next choice is EM, then MS, then SN, and the resulting cycle NEMSN costs $1060.

If you start at St. Louis, the first stop will be Evansville ($240 is the cheapest flight from St. Louis), then Memphis, then Nashville, the same cycle as the Evansville case (with a different starting point), costing $1040. From Memphis,  the cheapest leg is to Evansville, then Nashville, and finally St. Louis, for $1060—the same cycle as from Nashville, in the opposite direction.

To apply the sorted-edges algorithm, first sort the edges in order of increasing cost: EM($200), EN($220), ES($240), MN($260), MS ($300), NS($340). Edge EM is included, and so is EN. The next choice would be ES, but this is not allowed because its inclusion would give degree 3 to E. MN would complete a cycle of length 3 (too short), so the only other choices are MS and NS, forming route EMSNE (or ENSME) at a cost of $1060.

However, in this example, the best route is ENMSE, with cost $1020, and it does not arise from the nearest-neighbor algorithm, no matter which starting vertex is used, or from the sorted-edges algorithm.

The preceding example illustrates the fact that the two algorithms we have presented do not necessarily give the best-possible answer. However, both algorithms give quite good solutions in most cases.

You should also realize that there is no reason to expect the cycle obtained from the nearest-neighbor algorithm to be better or worse than the result of sorted edges;  sometimes one will be better, sometimes the other, and sometimes they will be the same.