حركة جسيم في مجال مغناطيسي ( قوة لورنتز)

سنتتبع حركة جسيم مشحون في مجال مغناطيسي كما يوضحها الشكل 1)). لقد عرفنا لتونا أن السرعة v لن يتغير مقدارها بتأثير القوة (وكل ما سيتغير هو اتجاه السرعة). فلو افترضنا الآن أن المجال المغناطيسي منتظم (أي أن له نفس الشدة ونفس الاتجاه في كل مكان) فإن مقدار القوة المغناطيسيةF = qvB . سيظل ثابتاً. إن عليك أن تثبت أن اتجاه القوة المبين في الشكل 1)) هو الاتجاه الصحيح.

لقد جابهنا في مرات عديدة من قبل موقفاً ديناميكياً مشابهاً. ومن ذلك حالتان كان فيهما الجسم تحت تأثير قوة ثابتة ومتعامدة باستمرار مع اتجاه الحركة وهما: (1) حالة كرة تتأرجح في دائرة وه معلقة في طرف خيط مثبت و (2) حالة الحركة في مدارات دائرية تثاقلية. والقوة في كل من هاتين الحالتين تجعل الجسم يتحرك في مسار دائري بسرعة ثابتة المقدار. وتوصف هذه الحركة بدلالة عجلة (تسارع) جذب مركزي هيv²/r  حيث r هو نصف قطر الحركة الدائرية. وفي الحالة الراهنة فإن القوة المسئولة عن هذه العجلة ( التسارع) هي qvB  ، أي القوة المغناطيسية المؤثرة على الشحنة q. ويتيح لنا قانون  نيوتن الثاني أن نكتب ما يلي:

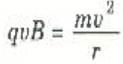
حيث m هي كتلة الجسيم المشحون. وعلى هذا تدور الشحنة q التي كتلتها m وتتحرك في مجال مغناطيسي منتظم B يتجه عمودياً على سرعة الشحنة v، في دائرة نصف قطرها:

 (1)       

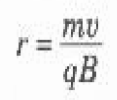
فإذا كانت الشحنة في الشكل ((1 سالبة فإن اتجاه القوة سينعكس وبذلك تدور الشحنة السالبة في دائرة في اتجاه حركة عقارب الساعة.

هناك فرق مهم جداً ، على المرء تذكره ، بين القوة الكهربية والقوى المغناطيسية المؤثرة على الشحنات ، ويمكن صياغة هذا الفرق كما يلي: