Scalar Wave Equation in a Schwarzschild Background

    We will be concerned with the behavior of quantum fields near horizons. In this lecture we will study the properties of a scalar wave equation in the background of a black hole.

     Let us consider a conventional massless free Klein–Gordon field χ in the Schwarzschild background. Here we will find great advantage in utilizing tortoise coordinates in which the metric has the form

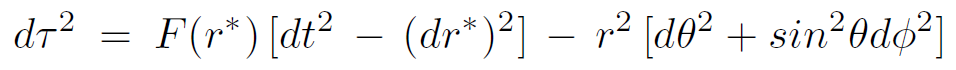 (1.1)

The action for χ is

 (1.2)

Now define

     ψ = r χ         (1.3)

and the action takes the form

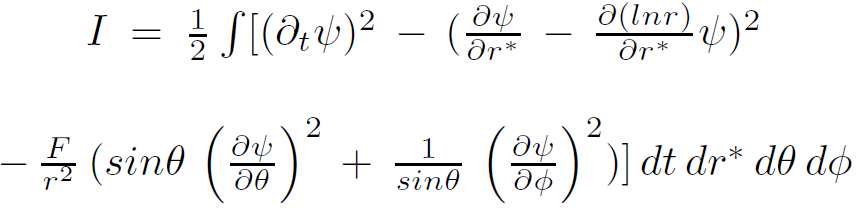 (1.4)

which, after an integration by parts and the introduction of spherical harmonic decomposition becomes

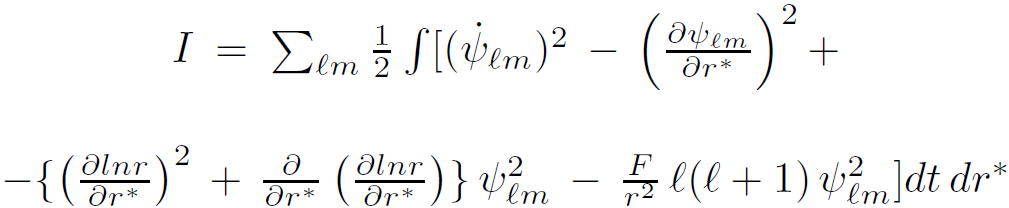(1.5)

Using the relation between r and r^∗

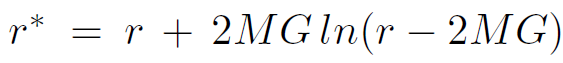
gives for each ℓ, m an action

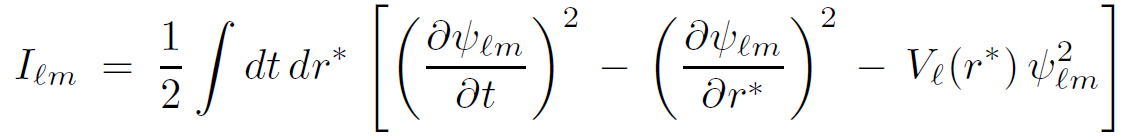 (1.6)

where the potential V_ℓ(r^∗) is given by

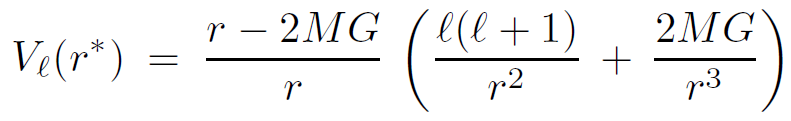 (1.7)

The equation of motion is

 (1.8)

and for a mode of frequency ν

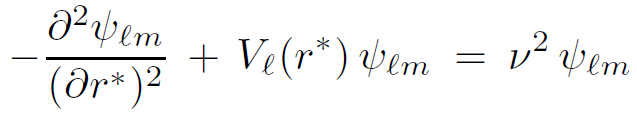 (1.9)

The potential V is shown in Figure 1.1 as a function of the Schwarzschild coordinate r. For r >> 3MG the potential is repulsive. In fact it is just the relativistic generalization of the usual repulsive centrifugal barrier. However as the horizon is approached, gravitational attraction wins and the potential becomes attractive, and pulls a wave packet toward the horizon. The maximum of the potential, where the direction of the force changes, depends weakly on the angular momentum ℓ.It is given by

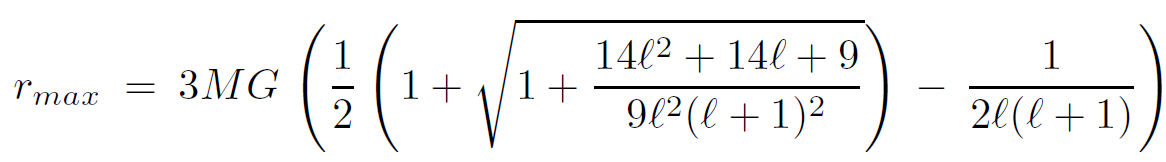 (1.10)

For ℓ→∞ the maximum occurs at r_max (ℓ→∞) = 3MG.

       The same potential governs the motion of massless classical particles. One can see that the points r_max(ℓ) represent unstable circular orbits, and

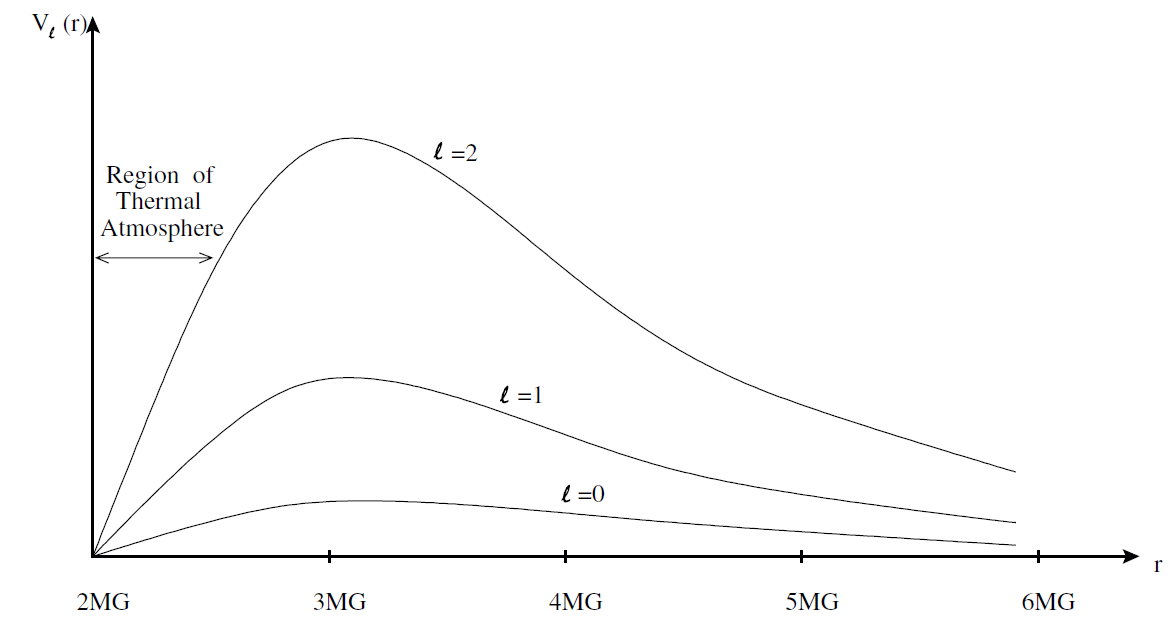
Fig. 1.1. Effective potential for free scalar field vs Schwarzschild radial coordinate.

the innermost such orbit is at r = 3MG.An y particle that starts with vanishing radial velocity in the region r < 3MG will spiral into the horizon.

    In the region of large negative r^∗ where we approach the horizon, the potential is unimportant, and the field behaves like a free massless Klein Gordon field. The eigenmodes in this region have the form of plane waves which propagate with unit velocity

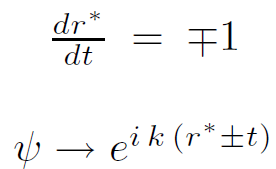(1.11)

Let us consider a field quantum of frequency ν and angular momentum ℓ propagating from large negative r^∗ toward the barrier at r ≈ 3MG.Will it pass over the barrier? To answer this we note that equation 1.9 has the form of a Schrodinger equation for a particle of energy ν² in a potential V . The particle has enough energy to overcome the barrier without tunneling if ν² is larger than the maximum height of the barrier. For example, if ℓ = 0 the height of the barrier is

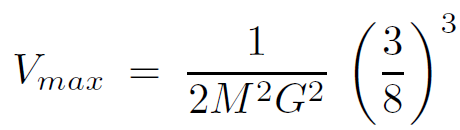 (1.12)

An s-wave quantum will therefore escape if

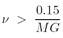 (1.13)

Similarly an s-wave quantum with ν > 0.15/MG will be able to penetrate the barrier from the outside and fall to the horizon. Less energetic particles must tunnel through the barrier.

        A particle of high angular momentum, whether on the inside or outside of the barrier will have more difficulty penetrating through. For large ℓ

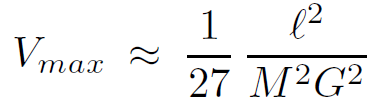 (1.14)

Therefore the threshold energy for passing over the barrier is

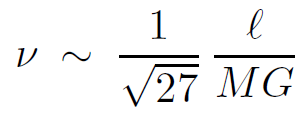 (1.15)