Kruskal-Szekeres Coordinates

Finally we can bring the black hole metric to the form

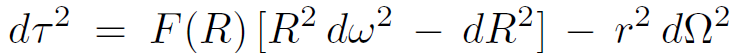 (1.1)

That ρ ≈ R. A more accurate comparison with the original Schwarzschild metric gives the following requirements:

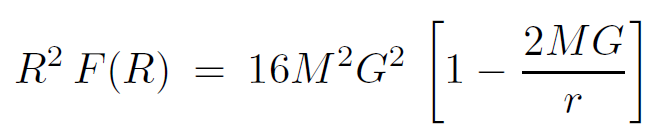 (1.2)

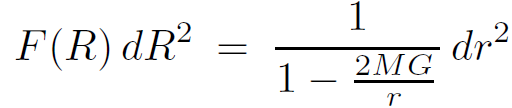 (1.3)

from which it follows that

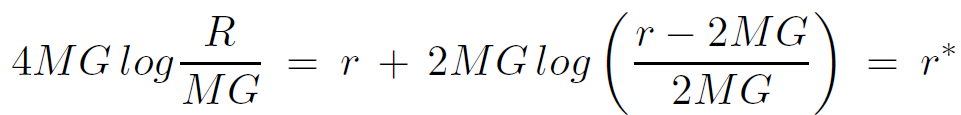 (1.4)

or

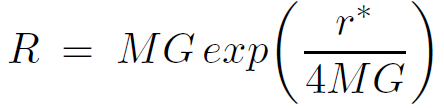 (1.5)

R and ω can be thought of as radial and hyperbolic angular coordinates of a space which is conformal to flat 1+1 dimensional Minkowski space. Letting

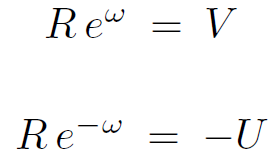 (1.6)

be “radial light-like” variables, the radial-time part of the metric takes the form

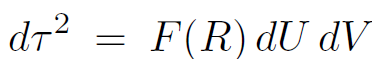 (1.7)

The coordinates U, V are shown in Figure 1.1. The surfaces of constant r are the time like hyperbolas in Figure 1.1. As r tends to 2MG the hyperbolas become the broken straight lines H+ and H− which we will call the extended past and future horizons. Although the extended horizons lie at finite values of the Kruskal-Szekeres coordinates, they are located at Schwarzschild time ±∞. Th us we see that a particle trajectory which crosses H⁺ in a finite proper time, crosses r = 2MG only after an infinite Schwarzschild time.

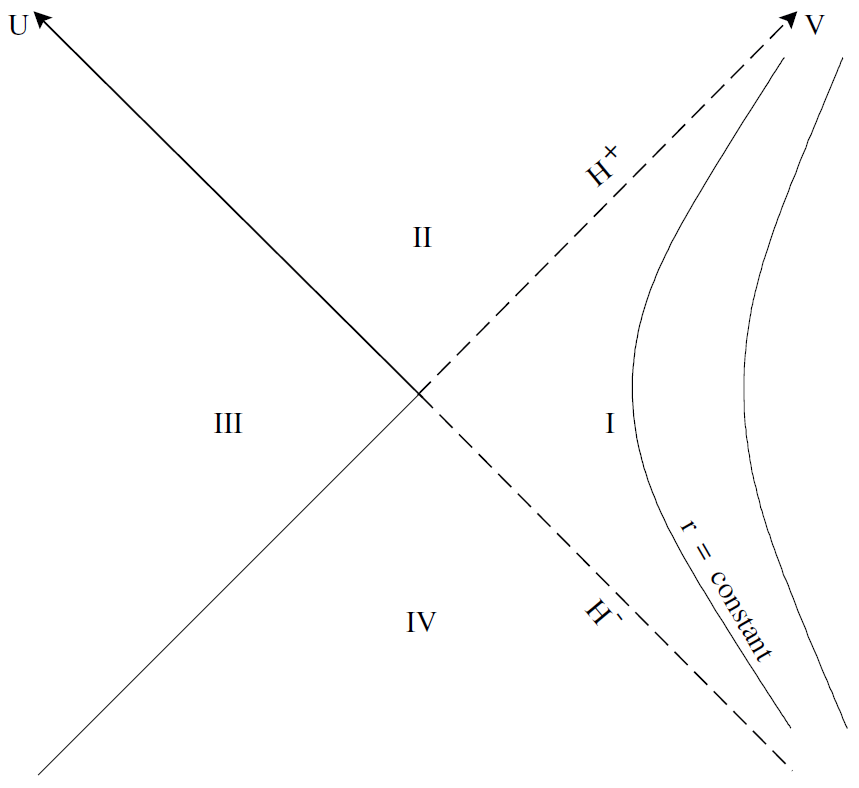
Fig. 1.1. U, V Kruskal-Szekeris coordinates.

     The region of Schwarzschild space with r < 2MG can be taken to be Region II.I n this region the surfaces of constant r are the space like hyperboloids

U V = positive constant (1.8)

The true singularity at r = 0 occurs at R² = −(MG)², or

    U V = (MG)²     (1.9)

The entire maximal analytic extension of the Schwarzschild geometry is easily described in Kruskal-Szekeres coordinates. It is shown in Figure 1.2.

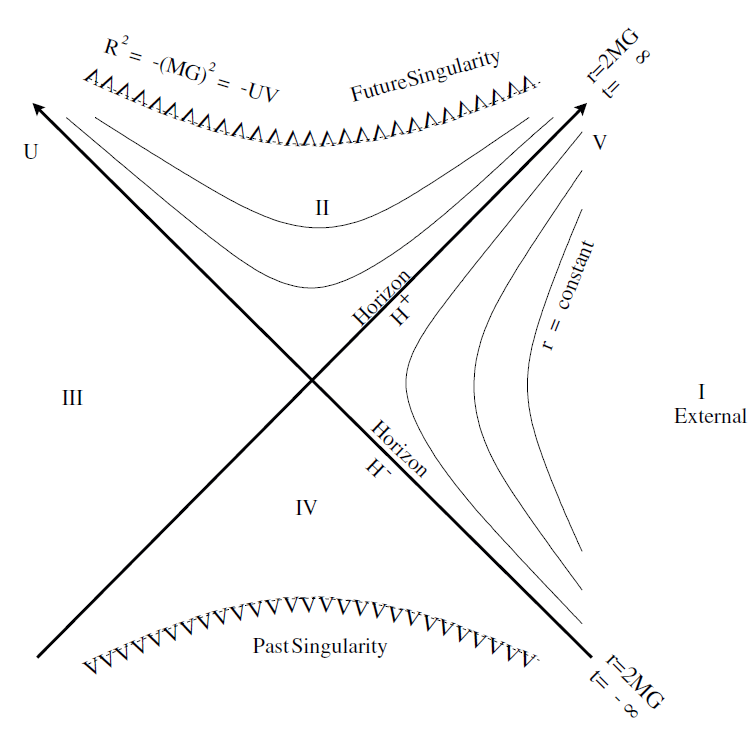
Fig. 1.2. Maximal analytic extension of Schwarzschild in Kruskal-Szekeris coordinates

A useful property of Kruskal-Szekeres coordinates is the fact that light rays and time like trajectories always lie within a two-dimensional light cone bounded by 45o lines. A radial moving light ray travels on a trajectory V = constant or U = constant. A non-radially directed light ray or time like trajectory always lies inside the two-dimensional light cone. With this in mind, it is easy to understand the causal properties of the black hole geometry. Consider a point P₁ in Region I. A radially outgoing light ray from P₁ will escape falling into the singularity as shown in Figure 1.3. An incoming light ray from P₁ will eventually cross H⁺ and then hit the future singularity. Thus an observer in Region I can send messages to infinity as well as into Region II.

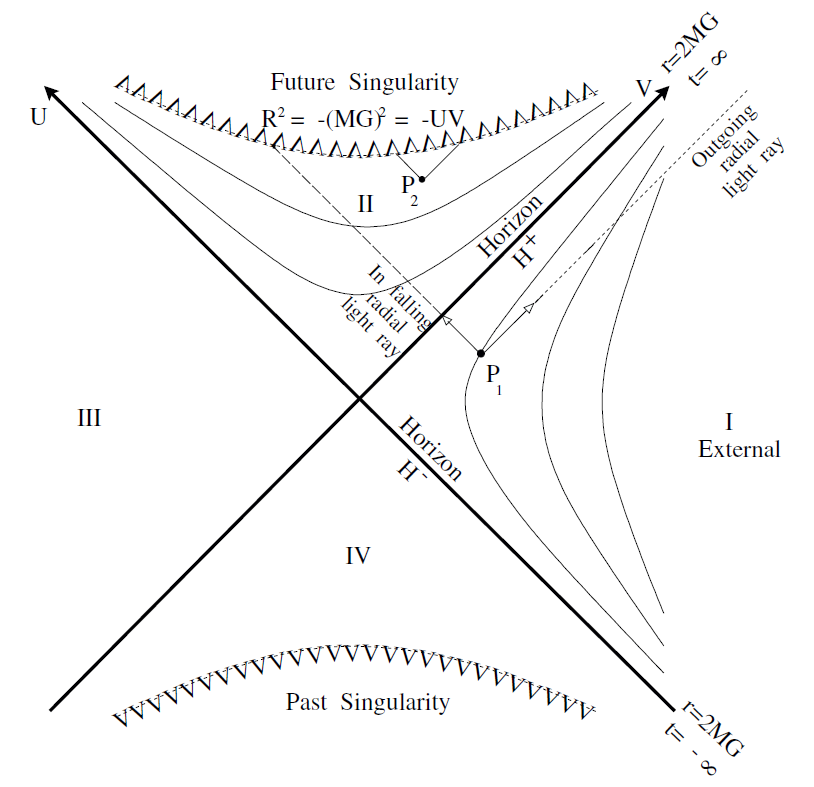
Fig. 1.3. Radial light rays from a point in Region I and Region II using Kruskal-Szekeris coordinates

      Consider next Region II. From any point P₂ any signal must eventually hit the singularity. Furthermore, no signal can ever escape to Region I. Thus no observer who stays outside r = 2MG can ever be influenced by events in Region II. For this reason Region II is said to be behind the horizon. Regions III and IV, as we will see, are not relevant to the classical problem of black holes formed by collapsing matter. Nevertheless let us consider them. From Region III no signal can ever get to Region I, and so it is also behind the horizon. On the other hand, points in Region IV can communicate with Region I. Region I however cannot communicate with Region IV. All of this is usually described by saying that Regions II and III are behind the future horizon while Regions III and IV are behind the past horizon.