The next example to be considered is the interesting situation of modes in two dimensions. Up to this point we have talked only about one-dimensional situations—a stretched string or sound waves in a tube. Ultimately, we should consider three dimensions, but an easier step will be that to two dimensions. Consider for definiteness a rectangular rubber drumhead which is confined so as to have no displacement anywhere on the rectangular edge, and let the dimensions of the rectangle be a and b, as shown in Fig. 49–4. Now the question is, what are the characteristics of the possible motion? We can start with the same procedure used for the string. If we had no confinement at all, we would expect waves travelling along with some kind of wave motion. For example, (e^iωt)(e^{−ik_xx+ik_yy}) would represent a sine wave travelling in some direction which depends on the relative values of k_x and k_y. Now how can we make the x-axis, that is, the line y=0, a node? Using the ideas developed for the one-dimensional string, we can imagine another wave represented by the complex function (− e^iωt)(e^{−ik_xx−ik_yy}). The superposition of these waves will give zero displacement at y=0 regardless of the values of x and t. (Although these functions are defined for negative y where there is no drumhead to vibrate, this can be ignored, since the displacement is truly zero at y=0.) In this case we can look upon the second function as the reflected wave.

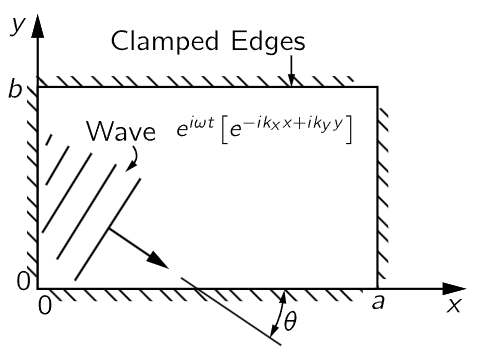
Fig. 49–4. Vibrating rectangular plate.

However, we want a nodal line at y=b as well as at y=0. How do we do that? The solution is related to something we did when studying reflection from crystals. These waves which cancel each other at y=0 will do the same at y=b only if 2b sinθ is an integral multiple of λ, where θ is the angle shown in Fig. 49–4:

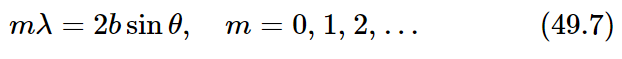
Now in the same way we can make the y-axis a nodal line by adding two more functions –(e^iωt)(e^+ik_xx+ik_yy) and +(e^iωt)(e^{+ik_xx−ik_yy}), each representing a reflection of one of the other two waves from the x=0 line. The condition for a nodal line at x=a is similar to the one for y=b. It is that 2a cosθ must also be an integral multiple of λ:

Then the final result is that the waves bouncing about in the box produce a standing-wave pattern, that is, a definite mode.

So we must satisfy the above two conditions if we are to have a mode. Let us first find the wavelength. This can be obtained by eliminating the angle θ from (49.7) and (49.8) to obtain the wavelength in terms of a, b, n and m. The easiest way to do that is to divide both sides of the respective equations by 2b and 2a, square them, and add the two equations together. The result is sin²θ+cos²θ=1=(nλ/2a)²+(mλ/2b)², which can be solved for λ:

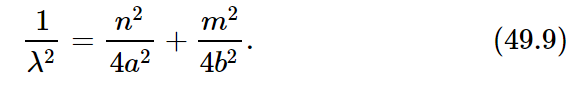
In this way we have determined the wavelength in terms of two integers, and from the wavelength we immediately get the frequency ω, because, as we know, the frequency is equal to 2πc divided by the wavelength.

This result is interesting and important enough that we should deduce it by a purely mathematical analysis instead of by an argument about the reflections. Let us represent the vibration by a superposition of four waves chosen so that the four lines x=0, x=a, y=0, and y=b are all nodes. In addition, we shall require that all waves have the same frequency, so that the resulting motion will represent a mode. From our earlier treatment of light reflection we know that (e^iωt)(e^{−ik_xx+ik_yy}) represents a wave travelling in the direction indicated in Fig. 49–4. Equation (49.6), that is, k=ω/c, still holds, provided

It is clear from the figure that k_x=k cosθ and k_y=k sinθ.

Now our equation for the displacement, say ϕ, of the rectangular drumhead takes on the grand form

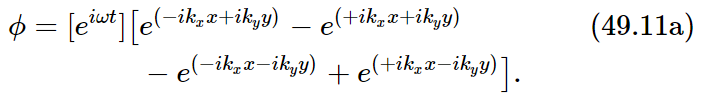
Although this looks rather a mess, the sum of these things now is not very hard. The exponentials can be combined to give sine functions, so that the displacement turns out to be

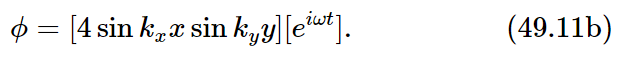
In other words, it is a sinusoidal oscillation, all right, with a pattern that is also sinusoidal in both the x- and the y-direction. Our boundary conditions are of course satisfied at x=0 and y=0. We also want ϕ to be zero when x=a and when y=b. Therefore, we have to put in two other conditions: k_xa must be an integral multiple of π, and k_yb must be another integral multiple of π. Since we have seen that k_x=k cosθ and k_y=k sinθ, we immediately get equations (49.7) and (49.8) and from these the final result (49.9).

Now let us take as an example a rectangle whose width is twice the height. If we take a=2b and use Eqs. (49.4) and (49.9), we can calculate the frequencies of all of the modes:

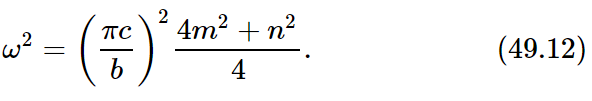
Table 49–1 lists a few of the simple modes and also shows their shape in a qualitative way.

Table 49–1

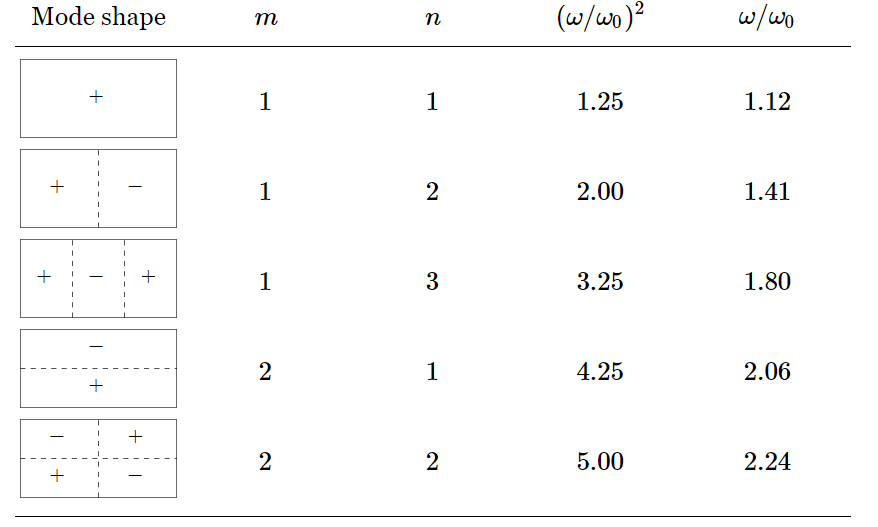
The most important point to be emphasized about this particular case is that the frequencies are not multiples of each other, nor are they multiples of any number. The idea that the natural frequencies are harmonically related is not generally true. It is not true for a system of more than one dimension, nor is it true for one-dimensional systems which are more complicated than a string with uniform density and tension. A simple example of the latter is a hanging chain in which the tension is higher at the top than at the bottom. If such a chain is set in harmonic oscillation, there are various modes and frequencies, but the frequencies are not simple multiples of any number, nor are the mode shapes sinusoidal.

The modes of more complicated systems are still more elaborate. For example, inside the mouth we have a cavity above the vocal cords, and by moving the tongue and the lips, and so forth, we make an open-ended pipe or a closed-ended pipe of different diameters and shapes; it is a terribly complicated resonator, but it is a resonator nevertheless. Now when one talks with the vocal cords, they are made to produce some kind of tone. The tone is rather complicated and there are many sounds coming out, but the cavity of the mouth further modifies that tone because of the various resonant frequencies of the cavity. For instance, a singer can sing various vowels, a, or o, or oo, and so forth, at the same pitch, but they sound different because the various harmonics are in resonance in this cavity to different degrees. The very great importance of the resonant frequencies of a cavity in modifying the voice sounds can be demonstrated by a simple experiment. Since the speed of sound goes as the reciprocal of the square root of the density, the speed of sound may be varied by using different gases. If one uses helium instead of air, so that the density is lower, the speed of sound is much higher, and all the frequencies of a cavity will be raised. Consequently, if one fills one’s lungs with helium before speaking, the character of his voice will be drastically altered even though the vocal cords may still be vibrating at the same frequency.