


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-10-15
التاريخ: 14-1-2023
التاريخ: 2023-10-15
التاريخ: 30-1-2022
|
The next interesting problem is to consider what happens if the string is held at both ends, say at x=0 and x=L. We can begin with the idea of the reflection of waves, starting with some kind of a bump moving in one direction. As time goes on, we would expect the bump to get near one end, and as time goes still further it will become a kind of little wobble, because it is combining with the reversed-image bump which is coming from the other side. Finally, the original bump will disappear and the image bump will move in the other direction to repeat the process at the other end. This problem has an easy solution, but an interesting question is whether we can have a sinusoidal motion (the solution just described is periodic, but of course it is not sinusoidally periodic). Let us try to put a sinusoidally periodic wave on a string. If the string is tied at one end, we know it must look like our earlier solution (49.3). If it is tied at the other end, it has to look the same at the other end. So, the only possibility for periodic sinusoidal motion is that the sine wave must neatly fit into the string length. If it does not fit into the string length, then it is not a natural frequency at which the string can continue to oscillate. In short, if the string is started with a sine wave shape that just fits in, then it will continue to keep that perfect shape of a sine wave and will oscillate harmonically at some frequency.
Mathematically, we can write sin kx for the shape, where k is equal to the factor (ω/c) in Eqs. (49.3) and (49.4), and this function will be zero at x=0. However, it must also be zero at the other end. The significance of this is that k is no longer arbitrary, as was the case for the half-open string. With the string closed at both ends, the only possibility is that sin(kL)=0, because this is the only condition that will keep both ends fixed. Now in order for a sine to be zero, the angle must be either 0, π, 2π, or some other integral multiple of π. The equation

will, therefore, give any one of the possible k’s, depending on what integer is put in. For each of the k’s there is a certain frequency ω, which, according to (49.3), is simply

So we have found the following: that a string has a property that it can have sinusoidal motions, but only at certain frequencies. This is the most important characteristic of confined waves. No matter how complicated the system is, it always turns out that there are some patterns of motion which have a perfect sinusoidal time dependence, but with frequencies that are a property of the particular system and the nature of its boundaries. In the case of the string we have many different possible frequencies, each one, by definition, corresponding to a mode, because a mode is a pattern of motion which repeats itself sinusoidally. Figure 49–2 shows the first three modes for a string. For the first mode the wavelength λ is 2L. This can be seen if one continues the wave out to x=2L to obtain one complete cycle of the sine wave. The angular frequency ω is 2πc divided by the wavelength, in general, and in this case, since λ is 2L, the frequency is πc/L, which is in agreement with (49.6) with n=1. Let us call the first mode frequency ω1. Now the next mode shows two loops with one node in the middle. For this mode the wavelength, then, is simply L. The corresponding value of k is twice as great and the frequency is twice as large; it is 2ω1. For the third mode it is 3ω1, and so on. So all the different frequencies of the string are multiples, 1, 2, 3, 4, and so on, of the lowest frequency ω1.
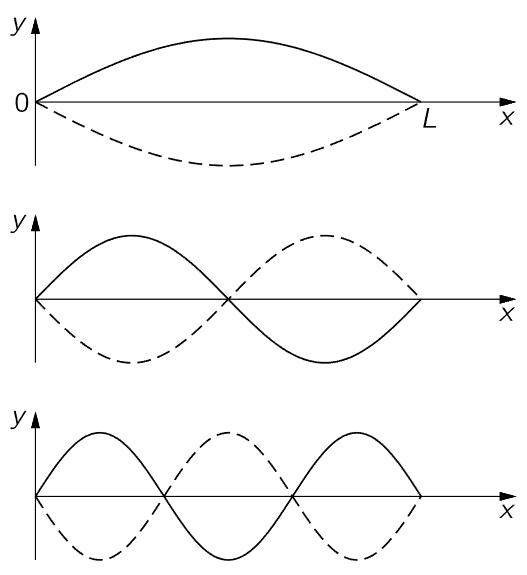
Fig. 49–2. The first three modes of a vibrating string.
Returning now to the general motion of the string, it turns out that any possible motion can always be analyzed by asserting that more than one mode is operating at the same time. In fact, for general motion an infinite number of modes must be excited at the same time. To get some idea of this, let us illustrate what happens when there are two modes oscillating at the same time: Suppose that we have the first mode oscillating as shown by the sequence of pictures in Fig. 49–3, which illustrates the deflection of the string for equally spaced time intervals extending through half a cycle of the lowest frequency.
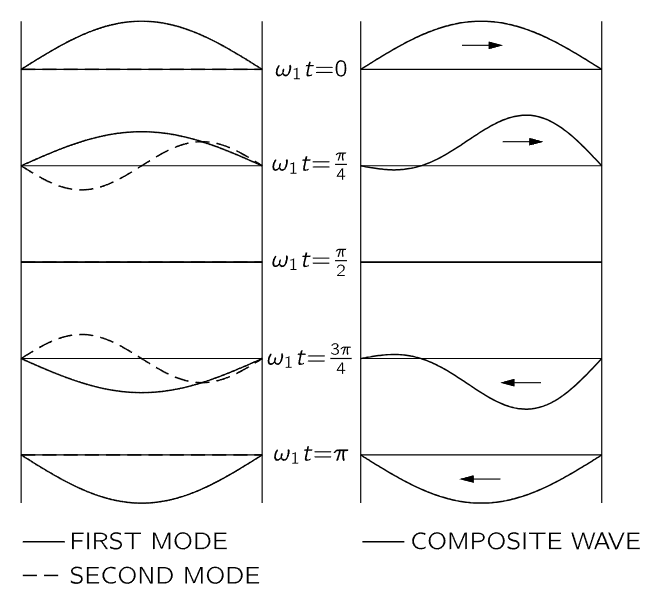
Fig. 49–3. Two modes combine to give a travelling wave.
Now, at the same time, we suppose that there is an oscillation of the second mode also. Figure 49–3 also shows a sequence of pictures of this mode, which at the start is 90∘ out of phase with the first mode. This means that at the start it has no displacement, but the two halves of the string have oppositely directed velocities. Now we recall a general principle relating to linear systems: if there are any two solutions, then their sum is also a solution. Therefore, a third possible motion of the string would be a displacement obtained by adding the two solutions shown in Fig. 49–3. The result, also shown in the figure, begins to suggest the idea of a bump running back and forth between the ends of the string, although with only two modes we cannot make a very good picture of it; more modes are needed. This result is, in fact, a special case of a great principle for linear systems:
Any motion at all can be analyzed by assuming that it is the sum of the motions of all the different modes, combined with appropriate amplitudes and phases.
The importance of the principle derives from the fact that each mode is very simple—it is nothing but a sinusoidal motion in time. It is true that even the general motion of a string is not really very complicated, but there are other systems, for example the whipping of an airplane wing, in which the motion is much more complicated. Nevertheless, even with an airplane wing, we find there is a certain particular way of twisting which has one frequency and other ways of twisting that have other frequencies. If these modes can be found, then the complete motion can always be analyzed as a superposition of harmonic oscillations (except when the whipping is of such degree that the system can no longer be considered as linear).



|
|
|
|
ما أبرز التغيرات التي تحدث عند الرجال عندما يصبحون آباءً؟
|
|
|
|
|
|
|
حقائق مثيرة للاهتمام حول الأرض
|
|
|
|
|
|
|
الأمانة العامة للعتبة الكاظمية المقدسة تشارك في انطلاق فعاليات أسبوع الولاية المُقام في قضاء الهاشمية
|
|
|