المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | خوارزمية القسمة Division Algorithm |
 10811
 09:35 صباحاً
التاريخ: 9-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 132|
أقرأ أيضاً
التاريخ: 19-11-2015
1508
التاريخ: 22-11-2015
2395
التاريخ: 4-11-2015
3901
التاريخ: 3-11-2015
1433
|
مفادها : أي عددين صحيحين مثل أ , ب , حيث ب> صفر يوجد عدد ان صحيحان آخران مثل جــ , د بحيث ان :
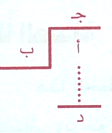
أ = (ب × جـ) + د
حيث صفر≼د >ب
ويسمى العدد جــ خارج القسمة
والعدد أ المقسوم
والدد ب المقسوم عليه
والعدد د الباقي من ناتج قسمة العدد أ على العدد ب
أي ان المقسوم = (المقسوم عليه × خارج القسمة) + الباقي
بالرموز أ = ( ب × جـ) + د
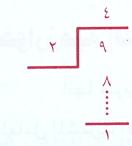
مثال :
9= (2×4) + 1
وتتسب هذه الطريقة إلى الخوارزمي (780 – 850) م الرياضي العربي واضع علم الجبر .
|
|
|
|
للتخلص من الإمساك.. فاكهة واحدة لها مفعول سحري
|
|
|
|
|
|
|
العلماء ينجحون لأول مرة في إنشاء حبل شوكي بشري وظيفي في المختبر
|
|
|
|
|
|
|
قسم العلاقات العامّة ينظّم برنامجاً ثقافياً لوفد من أكاديمية العميد لرعاية المواهب
|
|
|
