Our deduction of the wave equation for sound has given us a formula which connects the wave speed with the rate of change of pressure with the density at the normal pressure:

In evaluating this rate of change, it is essential to know how the temperature varies. In a sound wave, we would expect that in the region of compression the temperature would be raised, and that in the region of rarefaction the temperature would be lowered. Newton was the first to calculate the rate of change of pressure with density, and he supposed that the temperature remained unchanged. He argued that the heat was conducted from one region to the other so rapidly that the temperature could not rise or fall. This argument gives the isothermal speed of sound, and it is wrong. The correct deduction was given later by Laplace, who put forward the opposite idea—that the pressure and temperature change adiabatically in a sound wave. The heat flow from the compressed region to the rarefied region is negligible so long as the wavelength is long compared with the mean free path. Under this condition the slight amount of heat flow in a sound wave does not affect the speed, although it gives a small absorption of the sound energy. We can expect correctly that this absorption increases as the wavelength approaches the mean free path, but these wavelengths are smaller by factors of about a million than the wavelengths of audible sound.

The actual variation of pressure with density in a sound wave is the one that allows no heat flow. This corresponds to the adiabatic variation, which we found to be PV^γ=const, where V was the volume. Since the density ρ varies inversely with V, the adiabatic connection between P and ρ is

from which we get dP/dρ=_γP/ρ. We then have for the speed of sound the relation

We can also write c²_s=γPV/ρV and make use of the relation PV=NkT. Further, we see that ρV is the mass of gas, which can also be expressed as Nm, or as μ per mole, where m is the mass of a molecule and μ is the molecular weight. In this way we find that

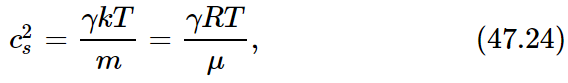
from which it is evident that the speed of sound depends only on the gas temperature and not on the pressure or the density. We also have observed that

where ⟨v²⟩ is the mean square of the speed of the molecules. It follows that c²_s=(γ/3)⟨v²⟩, or

This equation states that the speed of sound is some number which is roughly 1/(3)^1/2 times some average speed, v_av, of the molecules (the square root of the mean square velocity). In other words, the speed of sound is of the same order of magnitude as the speed of the molecules, and is actually somewhat less than this average speed.

Of course we could expect such a result, because a disturbance like a change in pressure is, after all, propagated by the motion of the molecules. However, such an argument does not tell us the precise propagation speed; it could have turned out that sound was carried primarily by the fastest molecules, or by the slowest molecules. It is reasonable and satisfying that the speed of sound is roughly 1/2 of the average molecular speed v_av.