


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 29-11-2020
التاريخ: 15-12-2016
التاريخ: 17-2-2016
التاريخ: 15-12-2016
|
In the preceding chapter we have presented a great many new ideas and results that play a central role in physics. These ideas are so important that it seems worthwhile to devote a whole chapter to a closer examination of them. In the present chapter we shall not repeat the “proofs” or the specific tricks by which the results were obtained, but shall concentrate instead upon a discussion of the ideas themselves.
In learning any subject of a technical nature where mathematics plays a role, one is confronted with the task of understanding and storing away in the memory a huge body of facts and ideas, held together by certain relationships which can be “proved” or “shown” to exist between them. It is easy to confuse the proof itself with the relationship which it establishes. Clearly, the important thing to learn and to remember is the relationship, not the proof. In any particular circumstance we can either say “it can be shown that” such and such is true, or we can show it. In almost all cases, the particular proof that is used is concocted, first of all, in such form that it can be written quickly and easily on the chalkboard or on paper, and so that it will be as smooth–looking as possible. Consequently, the proof may look deceptively simply, when in fact, the author might have worked for hours trying different ways of calculating the same thing until he has found the neatest way, so as to be able to show that it can be shown in the shortest amount of time! The thing to be remembered, when seeing a proof, is not the proof itself, but rather that it can be shown that such and such is true. Of course, if the proof involves some mathematical procedures or “tricks” that one has not seen before, attention should be given not to the trick exactly, but to the mathematical idea involved.
It is certain that in all the demonstrations that are made in a course such as this, not one has been remembered from the time when the author studied freshman physics. Quite the contrary: he merely remembers that such and such is true, and to explain how it can be shown he invents a demonstration at the moment it is needed. Anyone who has really learned a subject should be able to follow a similar procedure, but it is no use remembering the proofs. That is why, in this chapter, we shall avoid the proofs of the various statements made previously, and merely summarize the results.
The first idea that has to be digested is work done by a force. The physical word “work” is not the word in the ordinary sense of “Workers of the world unite!” but is a different idea. Physical work is expressed as ∫F⋅ds, called “the line integral of F dot ds,” which means that if the force, for instance, is in one direction and the object on which the force is working is displaced in a certain direction, then only the component of force in the direction of the displacement does any work. If, for instance, the force was constant and the displacement were a finite distance Δs, then the work done in moving the object through that distance is only the component of force along Δs times Δs. The rule is “force times distance,” but we really mean only the component of force in the direction of the displacement times Δs or, equivalently, the component of displacement in the direction of force times F. It is evident that no work whatsoever is done by a force which is at right angles to the displacement.
Now if the vector displacement Δs is resolved into components, in other words, if the actual displacement is Δs and we want to consider it effectively as a component of displacement Δx in the x–direction, Δy in the y–direction, and Δz in the z–direction, then the work done in carrying an object from one place to another can be calculated in three parts, by calculating the work done along x, along y, and along z. The work done in going along x involves only that component of force, namely Fx, and so on, so the work is FxΔx+FyΔy+FzΔz. When the force is not constant, and we have a complicated curved motion, then we must resolve the path into a lot of little Δs’s, add the work done in carrying the object along each Δs, and take the limit as Δs goes to zero. This is the meaning of the “line integral.”
Everything we have just said is contained in the formula W=∫F⋅ds. It is all very well to say that it is a marvelous formula, but it is another thing to understand what it means, or what some of the consequences are.
The word “work” in physics has a meaning so different from that of the word as it is used in ordinary circumstances that it must be observed carefully that there are some peculiar circumstances in which it appears not to be the same. For example, according to the physical definition of work, if one holds a hundred–pound weight off the ground for a while, he is doing no work. Nevertheless, everyone knows that he begins to sweat, shake, and breathe harder, as if he were running up a flight of stairs. Yet running upstairs is considered as doing work (in running downstairs, one gets work out of the world, according to physics), but in simply holding an object in a fixed position, no work is done. Clearly, the physical definition of work differs from the physiological definition, for reasons we shall briefly explore.
It is a fact that when one holds a weight he has to do “physiological” work. Why should he sweat? Why should he need to consume food to hold the weight up? Why is the machinery inside him operating at full throttle, just to hold the weight up? Actually, the weight could be held up with no effort by just placing it on a table; then the table, quietly and calmly, without any supply of energy, is able to maintain the same weight at the same height! The physiological situation is something like the following. There are two kinds of muscles in the human body and in other animals: one kind, called striated or skeletal muscle, is the type of muscle we have in our arms, for example, which is under voluntary control; the other kind, called smooth muscle, is like the muscle in the intestines or, in the clam, the greater adductor muscle that closes the shell. The smooth muscles work very slowly, but they can hold a “set”; that is to say, if the clam tries to close its shell in a certain position, it will hold that position, even if there is a very great force trying to change it. It will hold a position under load for hours and hours without getting tired because it is very much like a table holding up a weight, it “sets” into a certain position, and the molecules just lock there temporarily with no work being done, no effort being generated by the clam. The fact that we have to generate effort to hold up a weight is simply due to the design of striated muscle. What happens is that when a nerve impulse reaches a muscle fiber, the fiber gives a little twitch and then relaxes, so that when we hold something up, enormous volleys of nerve impulses are coming in to the muscle, large numbers of twitches are maintaining the weight, while the other fibers relax. We can see this, of course: when we hold a heavy weight and get tired, we begin to shake. The reason is that the volleys are coming irregularly, and the muscle is tired and not reacting fast enough. Why such an inefficient scheme? We do not know exactly why, but evolution has not been able to develop fast smooth muscle. Smooth muscle would be much more effective for holding up weights because you could just stand there and it would lock in; there would be no work involved and no energy would be required. However, it has the disadvantage that it is very slow–operating.
Returning now to physics, we may ask why we want to calculate the work done. The answer is that it is interesting and useful to do so, since the work done on a particle by the resultant of all the forces acting on it is exactly equal to the change in kinetic energy of that particle. That is, if an object is being pushed, it picks up speed, and
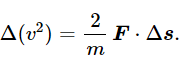



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|