


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-1-2022
Date: 16-1-2022
Date: 31-12-2021
|
A version of set theory which is a formal system expressed in first-order predicate logic. Zermelo-Fraenkel set theory is based on the Zermelo-Fraenkel axioms.
Zermelo-Fraenkel set theory is not finitely axiomatized. For example, the axiom of replacement is not really a single axiom, but an infinite family of axioms, since it is preceded by the stipulation that it is true "For any set-theoretic formula 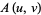 ." Montague (1961) proved that Zermelo-Fraenkel set theory is not finitely axiomatizable, i.e., there is no finite set of axioms which is logically equivalent to the infinite set of Zermelo-Fraenkel axioms. von Neumann-Bernays-Gödel set theory provides an equivalent finitely axiomized system.
." Montague (1961) proved that Zermelo-Fraenkel set theory is not finitely axiomatizable, i.e., there is no finite set of axioms which is logically equivalent to the infinite set of Zermelo-Fraenkel axioms. von Neumann-Bernays-Gödel set theory provides an equivalent finitely axiomized system.
REFERENCES:
Montague, R. "Semantic Closure and Non-Finite Axiomatizability. I." In Infinitistic Methods, Proceedings of the Symposium on Foundations of Mathematics, (Warsaw, 2-9 September 1959). Oxford, England: Pergamon, pp. 45-69, 1961.
Zermelo, E. "Über Grenzzahlen und Mengenbereiche." Fund. Math. 16, 29-47, 1930.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|