


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-11-2021
Date: 23-11-2021
Date: 29-11-2021
|
An algorithm for finding the nearest local minimum of a function which presupposes that the gradient of the function can be computed. The method of steepest descent, also called the gradient descent method, starts at a point 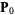 and, as many times as needed, moves from
and, as many times as needed, moves from 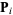 to
to 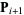 by minimizing along the line extending from
by minimizing along the line extending from 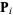 in the direction of
in the direction of 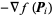 , the local downhill gradient.
, the local downhill gradient.
When applied to a 1-dimensional function 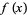 , the method takes the form of iterating
, the method takes the form of iterating
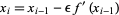 |
from a starting point 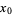 for some small
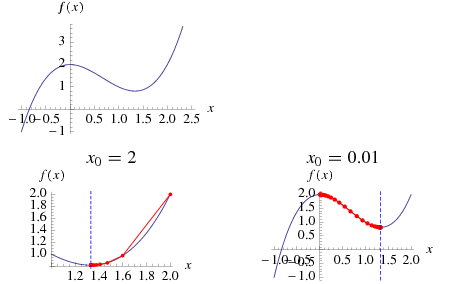
for some small 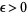 until a fixed point is reached. The results are illustrated above for the function
until a fixed point is reached. The results are illustrated above for the function 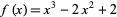 with
with 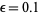 and starting points
and starting points 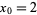 and 0.01, respectively.
and 0.01, respectively.
This method has the severe drawback of requiring a great many iterations for functions which have long, narrow valley structures. In such cases, a conjugate gradient method is preferable.
REFERENCES:
Arfken, G. "The Method of Steepest Descents." §7.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 428-436, 1985.
Menzel, D. (Ed.). Fundamental Formulas of Physics, Vol. 2, 2nd ed. New York: Dover, p. 80, 1960.
Morse, P. M. and Feshbach, H. "Asymptotic Series; Method of Steepest Descent." §4.6 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 434-443, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 414, 1992.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 985, 2002.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
خدمات متعددة يقدمها قسم الشؤون الخدمية للزائرين
|
|
|