


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-2-2016
Date: 16-2-2016
Date: 23-8-2021
|
In univariate interpolation, an interpolant is a function 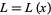 which agrees with a particular function
which agrees with a particular function 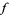 at a set of known points
at a set of known points 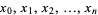 and which is used to compute values for
and which is used to compute values for 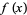 at points
at points 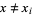 ,
, 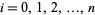 .
.
Modulo a change of notation, the above definition translates verbatim to multivariate interpolation models as well.
Generally speaking, the properties required of the interpolant are the most fundamental designations between various interpolation models. For example, the main difference between the linear and spline interpolation models is that the interpolant of the prior is required merely to be piecewise linear whereas spline interpolants are assumed to be piecewise polynomial and globally smooth.
REFERENCES:
Itô, K. (Ed.). "Interpolation." Section 223 (XV.2) in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 843-847, 1980.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|