


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2021
Date: 30-9-2021
Date: 21-12-2021
|
Differential entropy differs from normal or absolute entropy in that the random variable need not be discrete. Given a continuous random variable 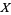 with a probability density function
with a probability density function 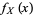 , the differential entropy
, the differential entropy 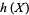 is defined as
is defined as
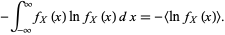 |
(1) |
When we have a continuous random vector 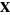 that consists of
that consists of 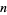 random variables
random variables 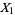 ,
, 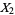 , ...,
, ..., 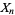 , the differential entropy of
, the differential entropy of 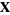 is defined as the
is defined as the 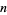 -fold integral
-fold integral
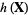 |
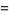 |
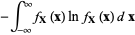 |
(2) |
 |
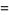 |
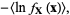 |
(3) |
where 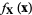 is the joint probability density function of
is the joint probability density function of 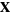 .
.
Thus, for example, the differential entropy of a multivariate Gaussian random variate 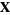 with covariance matrix
with covariance matrix 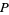 is
is
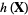 |
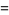 |
![1/2ln[(2pie)^n|det(P)|]](https://mathworld.wolfram.com/images/equations/DifferentialEntropy/Inline23.gif) |
(4) |
 |
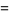 |
![1/2n[1+ln(2pi)]+1/2ln|det(P)|.](https://mathworld.wolfram.com/images/equations/DifferentialEntropy/Inline26.gif) |
(5) |
Additional properties of differential entropy include
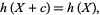 |
(6) |
where 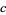 is a constant and
is a constant and
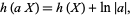 |
(7) |
where 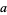 is a scaling factor and
is a scaling factor and 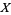 is a scalar random variable. The above property can be generalized to the case of a random vector
is a scalar random variable. The above property can be generalized to the case of a random vector 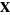 premultiplied by a matrix
premultiplied by a matrix 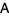 ,
,
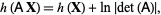 |
(8) |
where 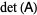 is the determinant of matrix
is the determinant of matrix 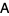 .
.
REFERENCES:
Cover, T. M. and Thomas, J. A. Elements of Information Theory. New York: Wiley, 1991.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|