


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-11-2021
Date: 16-8-2021
Date: 26-8-2021
|
A two-player game, also called crosscram, in which player 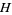 has horizontal dominoes and player
has horizontal dominoes and player 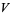 has vertical dominoes. The two players alternately place a domino on a board until the other cannot move, in which case the player having made the last move wins (Gardner 1974, Lachmann et al. 2000). Depending on the dimensions of the board, the winner will be
has vertical dominoes. The two players alternately place a domino on a board until the other cannot move, in which case the player having made the last move wins (Gardner 1974, Lachmann et al. 2000). Depending on the dimensions of the board, the winner will be 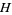 ,
, 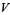 , 1 (the player making the first move), or 2 (the player making the second move). For example, the
, 1 (the player making the first move), or 2 (the player making the second move). For example, the 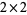 board is a win for the first player.
board is a win for the first player.
Berlekamp (1988) solved the general problem for 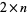 board for odd
board for odd 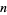 . Solutions for the
. Solutions for the 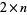 board are summarized in the following table, with
board are summarized in the following table, with 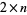 a win for
a win for 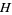 for
for 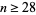 .
.
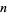 |
win | 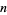 |
win | 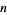 |
win |
| 0 | 2 | 10 | 1 | 20 | H |
| 1 | V | 11 | 1 | 21 | H |
| 2 | 1 | 12 | H | 22 | H |
| 3 | 1 | 13 | 2 | 23 | 1 |
| 4 | H | 14 | 1 | 24 | H |
| 5 | V | 15 | 1 | 25 | H |
| 6 | 1 | 16 | H | 26 | H |
| 7 | 1 | 17 | H | 27 | 1 |
| 8 | H | 18 | 1 | 28 | H |
| 9 | V | 19 | 1 | 29 | H |
Lachmann et al. (2000) have solved the game 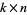 for widths of
for widths of 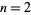 , 3, 4, 5, 7, 9, and 11, obtaining the results summarized in the following table for
, 3, 4, 5, 7, 9, and 11, obtaining the results summarized in the following table for 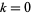 , 1, ....
, 1, ....
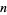 |
winner |
| 3 | 2, V, 1, 1, H, H, ... |
| 4 | H for even 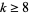 and all and all 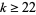 |
| 5 | 2, V, H, V, H, 2, H, H, ... |
| 7 | H for 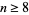 |
| 9 | H for 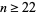 |
| 11 | H for 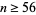 |
Bullock created a program called Obsequi that solved the additional cases 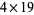 ,
,  ,
, 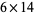 ,
, 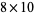 , and
, and 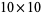 .
.
REFERENCES:
Berlekamp, E. R. "Blockbuster and Domineering." J. Combin. Th. Ser. A 49, 67-116, 1988.
Berlekamp, E. R.; Conway, J. H.; and Guy, R. K. Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.
Breuker, D. M.; Uiterwijk, J. W. H. M.; van den Herik, H. J. "Solving 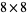 Domineering." Theor. Comput. Sci. 230, 195-206, 2000.
Domineering." Theor. Comput. Sci. 230, 195-206, 2000.
Bullock, N. "Obsequi's Domineering Page." http://www.cs.ualberta.ca/~games/domineering/.
Conway, J. H. On Numbers and Games, 2nd ed. Wellesley, MA: A K Peters, 2000.
Gardner, M. "Mathematical Games: Cram, Crosscram and Quadraphage: New Games having Elusive Winning Strategies." Sci. Amer. 230, 106-108, Feb. 1974.
Lachmann, M.; Moore, C.; and Rapaport, I. "Who Wins Domineering on Rectangular Boards?" 8 Jun 2000. http://arxiv.org/abs/math.CO/0006066.
Uiterwijk, J. W. H. M. and van den Herik, H. J. "The Advantage of the Initiative." Info. Sci. 122, 43-58, 2000.
Uiterwijk, J. W. H. M. "Domineering Results." http://www.cs.rulimburg.nl/~uiterwyk/Domineering_results.html.
Wolfe, D. "The Gamesman's Toolkit." In Games of No Chance, Proc. MSRI Workshop on Combinatorial Games, July, 1994 (Ed. R. J. Nowakowski). Cambridge, England: Cambridge University Press, 1998.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|