


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2021
Date: 19-11-2021
Date: 24-11-2021
|
A means of describing how one state develops into another state over the course of time. Technically, a dynamical system is a smooth action of the reals or the integers on another object (usually a manifold). When the reals are acting, the system is called a continuous dynamical system, and when the integers are acting, the system is called a discrete dynamical system. If 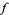 is any continuous function, then the evolution of a variable
is any continuous function, then the evolution of a variable  can be given by the formula
can be given by the formula
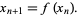 |
(1) |
This equation can also be viewed as a difference equation
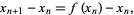 |
(2) |
so defining
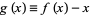 |
(3) |
gives
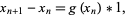 |
(4) |
which can be read "as 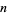 changes by 1 unit,
changes by 1 unit,  changes by
changes by 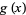 ." This is the discrete analog of the differential equation
." This is the discrete analog of the differential equation
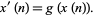 |
(5) |
REFERENCES:
Aoki, N. and Hiraide, K. Topological Theory of Dynamical Systems. Amsterdam, Netherlands: North-Holland, 1994.
Golubitsky, M. Introduction to Applied Nonlinear Dynamical Systems and Chaos. New York: Springer-Verlag, 1997.
Guckenheimer, J. and Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 3rd ed. New York: Springer-Verlag, 1997.
Jordan, D. W. and Smith, P. Nonlinear Ordinary Differential Equations: An Introduction to Dynamical Systems, 3rd ed. Oxford, England: Oxford University Press, 1999.
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion, 2nd ed. New York: Springer-Verlag, 1994.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, 1993.
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, 1990.
Strogatz, S. H. Nonlinear Dynamics and Chaos, with Applications to Physics, Biology, Chemistry, and Engineering. Reading, MA: Addison-Wesley, 1994.
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|