Surface of Section

A surface (or "space") of section, also called a Poincaré section (Rasband 1990, pp. 7 and 93-94), is a way of presenting a trajectory in 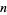-dimensional phase space in an 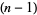-dimensional space. By picking one phase element constant and plotting the values of the other elements each time the selected element has the desired value, an intersection surface is obtained.

The above surface of section is for the Hénon-Heiles equation with energy 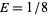 plotting  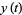vs. 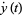 at values where .

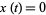If the equations of motion can be formulated as a map in which an explicit formula gives the values of the other elements at successive passages through the selected element value, the time required to compute the surface of section is greatly reduced.

REFERENCES:

Birkhoff, G. D. Dynamical Systems. Providence, RI: Amer. Math. Soc., 1927.

Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 143, 1988.

Poincaré, H. Les Methods Nouvelles de la Mécanique Celeste. Paris: Gauthier-Villars, 1892.

Rasband, S. N. "The Poincaré Map." §5.3 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, 1990.

Tabor, M. "The Surface of Section." §4.1 in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 118-126, 1989.