


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-8-2021
Date: 6-6-2021
Date: 13-7-2021
|

The above topological structure, composed of a countable union of compact sets, is called Alexander's horned sphere. It is homeomorphic with the ball 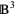 , and its boundary is therefore a sphere. It is therefore an example of a wild embedding in
, and its boundary is therefore a sphere. It is therefore an example of a wild embedding in 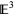 . The outer complement of the solid is not simply connected, and its fundamental group is not finitely generated. Furthermore, the set of nonlocally flat ("bad") points of Alexander's horned sphere is a Cantor set.
. The outer complement of the solid is not simply connected, and its fundamental group is not finitely generated. Furthermore, the set of nonlocally flat ("bad") points of Alexander's horned sphere is a Cantor set.
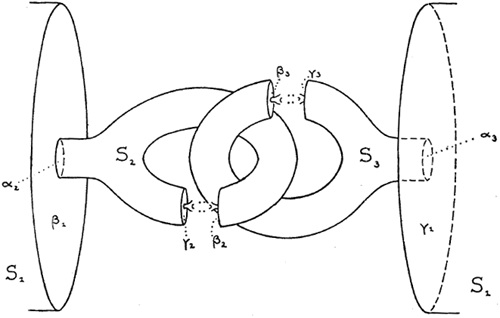
The horned sphere as originally drawn by Alexander (1924) is illustrated above.
The complement in 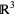 of the bad points for Alexander's horned sphere is simply connected, making it inequivalent to Antoine's horned sphere. Alexander's horned sphere has an uncountable infinity of wild points, which are the limits of the sequences of the horned sphere's branch points (roughly, the "ends" of the horns), since any neighborhood of a limit contains a horned complex.
of the bad points for Alexander's horned sphere is simply connected, making it inequivalent to Antoine's horned sphere. Alexander's horned sphere has an uncountable infinity of wild points, which are the limits of the sequences of the horned sphere's branch points (roughly, the "ends" of the horns), since any neighborhood of a limit contains a horned complex.

A humorous drawing by Simon Fraser (Guy 1983, Schroeder 1991, Albers 1994) depicts mathematician John H. Conway with Alexander's horned sphere growing from his head.
REFERENCES:
Albers, D. J. Illustration accompanying "The Game of 'Life.' " Math Horizons, p. 9, Spring 1994.
Alexander, J. W. "An Example of a Simply Connected Surface Bounding a Region Which Is Not Simply Connected." Proc. N. A. S. 10, 8-10, 1924.
Guy, R. "Conway's Prime Producing Machine." Math. Mag. 56, 26-33, 1983.
Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 80-81, 1976.
Schroeder, M. Fractals, Chaos, Power Law: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 58, 1991.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|