Sutured Manifold

A sutured manifold is a tool in geometric topology which was first introduced by David Gabai in order to study taut foliations on 3-manifolds. Roughly, a sutured manifold is a pair 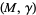 with 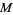 a compact, oriented 3-manifold with boundary and with  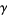a set of simple closed curves in  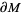which are oriented and which divide  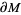into pieces  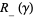and 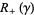 (Juhász 2010).

Defined precisely in a seminal work by Gabai (1983), a sutured manifold 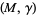 is a compact oriented 3-manifold  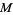together with a set  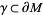of pairwise disjoint annuli  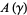and tori  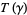such that each component of  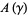contains a homologically nontrivial oriented simple closed curve (called a suture) and such that  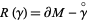is oriented. 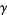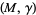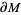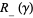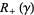Using this construction, the collection  of a sutured manifold  effectively splits  into disjoint pieces  and  with 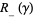, respectively 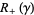, defined to be the components of  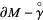whose normal vectors point into, respectively point out of, 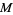. Gabai's definition also requires that orientations on  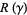be coherent with respect to the set  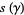of sutures in the sense that any component  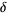of 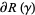 with boundary orientation must represent the same homology class in  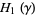as some suture.

The study of sutured 3-manifolds has yielded several strong results and continues to be an important focus of research among topologists today. For example, Gabai's work on sutured 3-manifolds provided the framework necessary to obtain answers to several longstanding problems including the Poenaru conjecture and the Property R conjecture, as well as a number of knot-theoretic problems including the superadditivity of knot genus and property P for satellite knots (Scharlemann 1989). In addition, sutured 3-manifolds which are balanced (i.e., those manifolds 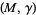 which have no closed components, for which each component of  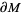contains a suture, and for which  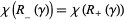where 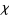 denotes the Euler characteristic) have also been studied in the context of so-called sutured Floer homology, an invariant of balanced sutured manifolds and a generalization of both Heegaard Floer homology and knot Floer homology (Juhász 2010).

REFERENCES:

Gabai, D. "Foliations and the Topology of 3-Manifolds." J. Diff. Geom. 18, 445-503, 1983.

Juhász, A. "Problems in Sutured Floehr Homology." 2010. https://www.dpmms.cam.ac.uk/~aij22/SFH_problems.pdf.

Scharlemann, M. "Sutured Manifolds and Generalized Thurston Norms." J. Diff. Geom. 29, 557-614, 1989.