


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-7-2021
Date: 20-7-2021
Date: 6-7-2021
|
Mergelyan's theorem can be stated as follows (Krantz 1999). Let 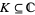 be compact and suppose
be compact and suppose 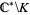 has only finitely many connected components. If
has only finitely many connected components. If 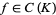 is holomorphic on the interior of
is holomorphic on the interior of 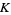 and if
and if 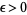 , then there is a rational function
, then there is a rational function 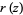 with poles in
with poles in 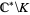 such that
such that
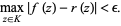 |
(1) |
A consequence is that if 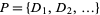 is an infinite set of disjoint open disks
is an infinite set of disjoint open disks 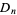 of radius
of radius 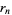 such that the union is almost the unit disk. Then
such that the union is almost the unit disk. Then
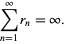 |
(2) |
Define
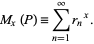 |
(3) |
Then there is a number 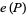 such that
such that 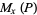 diverges for
diverges for 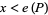 and converges for
and converges for 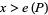 . The above theorem gives
. The above theorem gives
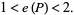 |
(4) |
There exists a constant which improves the inequality, and the best value known is
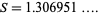 |
(5) |
REFERENCES:
Krantz, S. G. "Mergelyan's Theorem." §11.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 146-147, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 36-37, 1983.
Mandelbrot, B. B. Fractals. San Francisco, CA: W. H. Freeman, p. 187, 1977.
Melzack, Z. A. "On the Solid Packing Constant for Circles." Math. Comput. 23, 1969.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|