
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-5-2021
Date: 13-5-2021
Date: 22-7-2021
|
Let 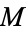 be a Riemannian manifold, and let the topological metric on
be a Riemannian manifold, and let the topological metric on 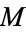 be defined by letting the distance between two points be the infimum of the lengths of curves joining the two points. The Hopf-Rinow theorem then states that the following are equivalent:
be defined by letting the distance between two points be the infimum of the lengths of curves joining the two points. The Hopf-Rinow theorem then states that the following are equivalent:
1. 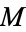 is geodesically complete, i.e., all geodesics are defined for all time.
is geodesically complete, i.e., all geodesics are defined for all time.
2. 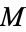 is geodesically complete at some point
is geodesically complete at some point 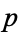 , i.e., all geodesics through
, i.e., all geodesics through 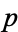 are defined for all time.
are defined for all time.
3. 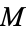 satisfies the Heine-Borel property, i.e., every closed bounded set is compact.
satisfies the Heine-Borel property, i.e., every closed bounded set is compact.
4. 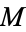 is metrically complete.
is metrically complete.
REFERENCES:
Petersen, P. Riemannian Geometry. New York: Springer Verlag, p. 125, 1998.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|