


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-5-2021
Date: 24-5-2021
Date: 7-8-2021
|
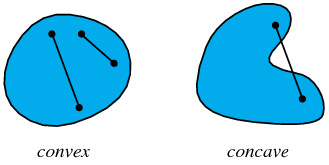
A set in Euclidean space 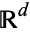 is convex set if it contains all the line segments connecting any pair of its points. If the set does not contain all the line segments, it is called concave.
is convex set if it contains all the line segments connecting any pair of its points. If the set does not contain all the line segments, it is called concave.
A convex set is always star convex, implying pathwise-connected, which in turn implies connected.
A region can be tested for convexity in the Wolfram Language using the function Region`ConvexRegionQ[reg].
REFERENCES:
Benson, R. V. Euclidean Geometry and Convexity. New York: McGraw-Hill, 1966.
Busemann, H. Convex Surfaces. New York: Interscience, 1958.
Croft, H. T.; Falconer, K. J.; and Guy, R. K. "Convexity." Ch. A in Unsolved Problems in Geometry. New York: Springer-Verlag, pp. 6-47, 1994.
Eggleston, H. G. Problems in Euclidean Space: Applications of Convexity. New York: Pergamon Press, 1957.
Gruber, P. M. "Seven Small Pearls from Convexity." Math. Intell. 5, 16-19, 1983.
Gruber, P. M. "Aspects of Convexity and Its Applications." Expos. Math. 2, 47-83, 1984.
Guggenheimer, H. Applicable Geometry--Global and Local Convexity. New York: Krieger, 1977.
Kelly, P. J. and Weiss, M. L. Geometry and Convexity: A Study of Mathematical Methods. New York: Wiley, 1979.
Webster, R. Convexity. Oxford, England: Oxford University Press, 1995.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|