


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-6-2021
Date: 24-6-2021
Date: 14-7-2021
|
A Kähler structure on a complex manifold 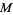 combines a Riemannian metric on the underlying real manifold with the complex structure. Such a structure brings together geometry and complex analysis, and the main examples come from algebraic geometry. When
combines a Riemannian metric on the underlying real manifold with the complex structure. Such a structure brings together geometry and complex analysis, and the main examples come from algebraic geometry. When 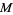 has
has 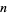 complex dimensions, then it has
complex dimensions, then it has 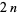 real dimensions. A Kähler structure is related to the unitary group
real dimensions. A Kähler structure is related to the unitary group 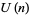 , which embeds in
, which embeds in 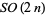 as the orthogonal matrices that preserve the almost complex structure (multiplication by '
as the orthogonal matrices that preserve the almost complex structure (multiplication by '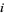 '). In a coordinate chart, the complex structure of
'). In a coordinate chart, the complex structure of 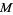 defines a multiplication by
defines a multiplication by 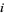 and the metric defines orthogonality for tangent vectors. On a Kähler manifold, these two notions (and their derivatives) are related.
and the metric defines orthogonality for tangent vectors. On a Kähler manifold, these two notions (and their derivatives) are related.
The following are elements of a Kähler structure, with each condition sufficient for a Kähler structure to exist.
1. A Kähler metric. Near any point 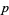 , there exists holomorphic coordinates
, there exists holomorphic coordinates 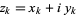 such that the metric has the form
such that the metric has the form
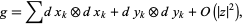 |
(1) |
where  denotes the vector space tensor product; that is, it vanishes up to order two at
denotes the vector space tensor product; that is, it vanishes up to order two at 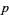 . Hence any geometric equation in
. Hence any geometric equation in 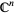 involving only the first derivatives can be defined on a Kähler manifold. Note that a generic metric can be written to vanish up to order two, but not necessarily in holomorphic coordinates, using a Gaussian coordinate system.
involving only the first derivatives can be defined on a Kähler manifold. Note that a generic metric can be written to vanish up to order two, but not necessarily in holomorphic coordinates, using a Gaussian coordinate system.
2. A Kähler form 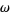 is a real closed nondegenerate two-form, i.e., a symplectic form, for which
is a real closed nondegenerate two-form, i.e., a symplectic form, for which 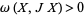 for nonzero tangent vectors
for nonzero tangent vectors 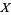 . Moreover, it must also satisfy
. Moreover, it must also satisfy 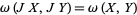 , where
, where 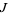 is the almost complex structure induced by multiplication by
is the almost complex structure induced by multiplication by 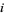 . That is,
. That is,
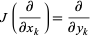 |
(2) |
and
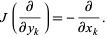 |
(3) |
Locally, a Kähler form can be written as 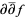 , where
, where 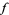 is a function called a Kähler potential. The Kähler form is a real
is a function called a Kähler potential. The Kähler form is a real 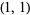 -complex form.
-complex form.
3. A Hermitian metric 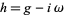 where the real part is a Kähler metric, as in item (1) above, and where the imaginary part is a Kähler form, as in item (2).
where the real part is a Kähler metric, as in item (1) above, and where the imaginary part is a Kähler form, as in item (2).
4. A metric for which the almost complex structure 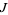 is parallel. Since parallel transport is always an isometry, a Hermitian metric is well-defined by parallel transport along paths from a base point. The holonomy group is contained in the unitary group.
is parallel. Since parallel transport is always an isometry, a Hermitian metric is well-defined by parallel transport along paths from a base point. The holonomy group is contained in the unitary group.
It is easy to see that a complex submanifold of a Kähler manifold inherits its Kähler structure, and so must also be Kähler. The main source of examples are projective algebraic varieties, complex submanifolds of complex projective space which are solutions to algebraic equations.
There are several deep consequences of the Kähler condition. For example, the Kähler identities, the Hodge decomposition of cohomology, and the Lefschetz theorem depends on the Kähler condition for compact manifolds.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|