


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-7-2021
Date: 24-5-2021
Date: 24-7-2021
|
Given a principal bundle  , with fiber a Lie group
, with fiber a Lie group  and base manifold
and base manifold  , and a group representation of
, and a group representation of  , say
, say 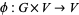 , then the associated vector bundle is
, then the associated vector bundle is
 |
(1) |
In particular, it is the quotient space  where
where 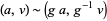 .
.
This construction has many uses. For instance, any group representation of the orthogonal group gives rise to a bundle of tensors on a Riemannian manifold as the vector bundle associated to the frame bundle.
For example, 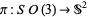 is the frame bundle on
is the frame bundle on 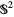 , where
, where
![pi([w_1; w_2; w_3])=w_1,](https://mathworld.wolfram.com/images/equations/AssociatedVectorBundle/NumberedEquation2.gif) |
(2) |
writing the special orthogonal matrix with rows  . It is a
. It is a  bundle with the action defined by
bundle with the action defined by
![[costheta -sintheta; sintheta costheta]·A=[1 0 0; 0 costheta -sintheta; 0 sintheta costheta]A,](https://mathworld.wolfram.com/images/equations/AssociatedVectorBundle/NumberedEquation3.gif) |
(3) |
which preserves the map 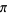 .
.
The tangent bundle is the associated vector bundle with the standard group representation of  on
on 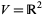 , given by pairs
, given by pairs 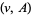 , with
, with  and
and 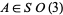 . Two pairs
. Two pairs  and
and 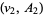 represent the same tangent vector iff there is a
represent the same tangent vector iff there is a 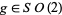 such that
such that 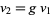 and
and  .
.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة توجه دعوة لجامعة القادسية للمشاركة في حفل التخرج المركزي
|
|
|