Planck's Radiation Function

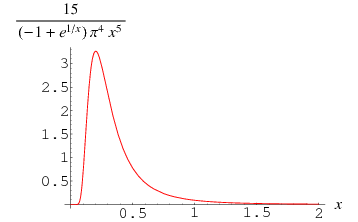
Planck's's radiation function is the function

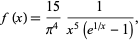(1)

which is normalized so that

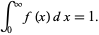(2)

However, the function is sometimes also defined without the numerical normalization factor of 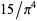 (e.g., Abramowitz and Stegun 1972, p. 999).

The first and second raw moments are

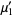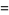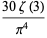			(3)
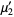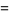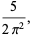			(4)

where 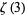 is Apéry's constant, but higher order raw moments do not exist since the corresponding integrals do not converge.

It has a maximum at 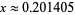 (OEIS A133838), where

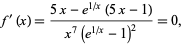(5)

and inflection points at 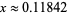 (OEIS A133839) and  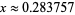(OEIS A133840), where

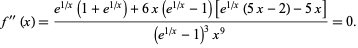(6)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Planck's Radiation Function." §27.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 999, 1972.

Sloane, N. J. A. Sequences A133838, A133839, A133840 in "The On-Line Encyclopedia of Integer Sequences."