


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-4-2021
Date: 1-5-2021
Date: 2-3-2021
|
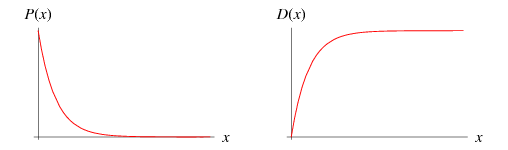
Given a Poisson distribution with rate of change 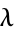 , the distribution of waiting times between successive changes (with
, the distribution of waiting times between successive changes (with 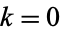 ) is
) is
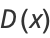 |
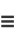 |
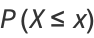 |
(1) |
 |
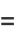 |
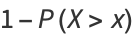 |
(2) |
 |
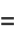 |
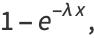 |
(3) |
and the probability distribution function is
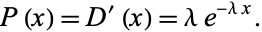 |
(4) |
It is implemented in the Wolfram Language as ExponentialDistribution[lambda].
The exponential distribution is the only continuous memoryless random distribution. It is a continuous analog of the geometric distribution.
This distribution is properly normalized since
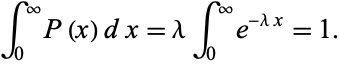 |
(5) |
The raw moments are given by
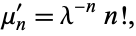 |
(6) |
the first few of which are therefore 1, 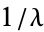 ,
, 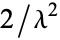 ,
, 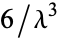 ,
, 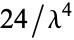 , .... Similarly, the central moments are
, .... Similarly, the central moments are
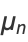 |
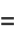 |
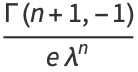 |
(7) |
 |
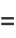 |
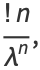 |
(8) |
where 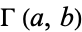 is an incomplete gamma function and
is an incomplete gamma function and 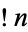 is a subfactorial, giving the first few as 1, 0,
is a subfactorial, giving the first few as 1, 0, 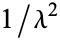 ,
, 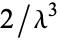 ,
, 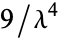 ,
, 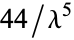 , ... (OEIS A000166).
, ... (OEIS A000166).
The mean, variance, skewness, and kurtosis excess are therefore
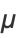 |
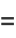 |
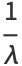 |
(9) |
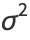 |
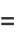 |
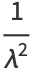 |
(10) |
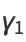 |
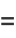 |
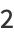 |
(11) |
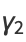 |
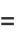 |
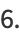 |
(12) |
The characteristic function is
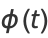 |
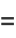 |
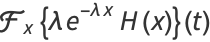 |
(13) |
 |
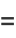 |
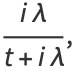 |
(14) |
where 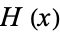 is the Heaviside step function and
is the Heaviside step function and ](https://mathworld.wolfram.com/images/equations/ExponentialDistribution/Inline47.gif) is the Fourier transform with parameters
is the Fourier transform with parameters 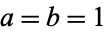 .
.
If a generalized exponential probability function is defined by
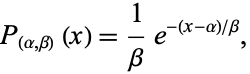 |
(15) |
for 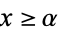 , then the characteristic function is
, then the characteristic function is
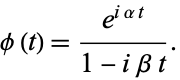 |
(16) |
The central moments are
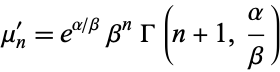 |
(17) |
and the raw moments are
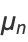 |
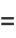 |
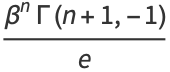 |
(18) |
 |
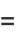 |
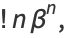 |
(19) |
and the mean, variance, skewness, and kurtosis excess are
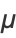 |
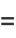 |
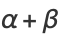 |
(20) |
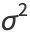 |
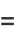 |
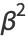 |
(21) |
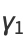 |
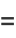 |
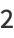 |
(22) |
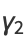 |
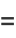 |
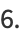 |
(23) |
REFERENCES:
Balakrishnan, N. and Basu, A. P. The Exponential Distribution: Theory, Methods, and Applications. New York: Gordon and Breach, 1996.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 534-535, 1987.
Sloane, N. J. A. Sequence A000166/M1937 in "The On-Line Encyclopedia of Integer Sequences."
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 119, 1992.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|