


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-3-2021
Date: 9-2-2021
Date: 27-3-2021
|
Let 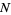 samples be taken from a population with central moments
samples be taken from a population with central moments 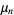 . The sample variance
. The sample variance 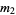 is then given by
is then given by
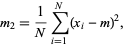 |
(1) |
where 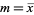 is the sample mean.
is the sample mean.
The expected value of 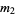 for a sample size
for a sample size 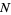 is then given by
is then given by
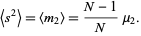 |
(2) |
Similarly, the expected variance of the sample variance is given by
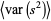 |
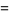 |
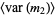 |
(3) |
 |
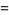 |
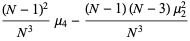 |
(4) |
(Kenney and Keeping 1951, p. 164; Rose and Smith 2002, p. 264).
The algebra of deriving equation (4) by hand is rather tedious, but can be performed as follows. Begin by noting that
 |
(5) |
so
 |
(6) |
The value of  is already known from equation (◇), so it remains only to find
is already known from equation (◇), so it remains only to find 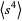 . The algebra is simplified considerably by immediately transforming variables to
. The algebra is simplified considerably by immediately transforming variables to 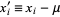 and performing computations with respect to these central variables. Since the variance does not depend on the mean
and performing computations with respect to these central variables. Since the variance does not depend on the mean 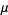 of the underlying distribution, the result obtained using the transformed variables will give an identical result while immediately eliminating expectation values of sums of terms containing odd powers of
of the underlying distribution, the result obtained using the transformed variables will give an identical result while immediately eliminating expectation values of sums of terms containing odd powers of 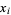 (which equal 0). To determine
(which equal 0). To determine 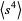 , expand equation (6) to obtain
, expand equation (6) to obtain
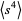 |
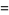 |
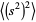 |
(7) |
 |
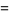 |
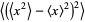 |
(8) |
 |
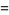 |
![<[1/Nsumx_i^2-(1/Nsumx_i)^2]^2>](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline27.gif) |
(9) |
 |
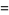 |
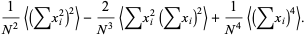 |
(10) |
Working on the first term of (10),
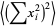 |
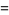 |
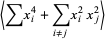 |
(11) |
 |
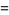 |
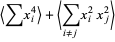 |
(12) |
 |
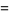 |
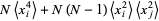 |
(13) |
 |
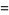 |
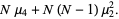 |
(14) |
The second term of (◇) is given by
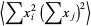 |
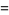 |
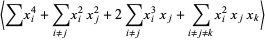 |
(15) |
 |
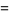 |
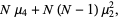 |
(16) |
and the third term by
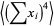 |
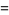 |
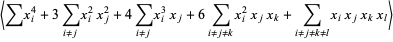 |
(17) |
 |
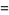 |
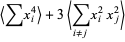 |
(18) |
 |
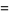 |
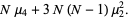 |
(19) |
Plugging (◇)-(19) into (◇) then gives
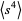 |
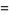 |
![1/(N^2)[Nmu_4+N(N-1)mu_2^2]-2/(N^3)[Nmu_4+N(N-1)mu_2^2]+1/(N^4)[Nmu_4+3N(N-1)mu_2^2]](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline60.gif) |
(20) |
 |
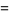 |
![(1/N-2/(N^2)+1/(N^3))mu_4+[(N-1)/N-(2(N-1))/(N^2)+(3(N-1))/(N^3)]mu_2^2](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline63.gif) |
(21) |
 |
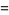 |
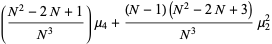 |
(22) |
 |
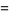 |
![((N-1)[(N-1)mu_4+(N^2-2N+3)mu_2^2])/(N^3)](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline69.gif) |
(23) |
(Kenney and Keeping 1951, p. 164). Plugging (◇) and (23) into (◇) then gives
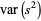 |
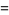 |
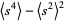 |
(24) |
 |
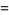 |
![((N-1)[(N-1)mu_4-(N-3)mu_2^2])/(N^3),](https://mathworld.wolfram.com/images/equations/SampleVarianceDistribution/Inline75.gif) |
(25) |
as before.
For a normal distribution, 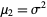 and
and 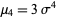 , so
, so
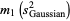 |
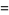 |
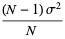 |
(26) |
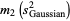 |
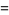 |
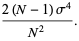 |
(27) |
The third ane fourth moments of 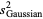 are given by
are given by
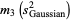 |
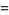 |
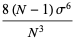 |
(28) |
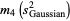 |
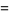 |
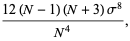 |
(29) |
giving the skewness and kurtosis excess of the distribution of the 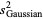 as
as
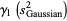 |
 |
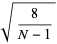 |
(30) |
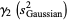 |
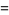 |
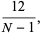 |
(31) |
as computed by Student. Student also conjectured that the underlying distribution is Pearson type III distribution
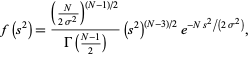 |
(32) |
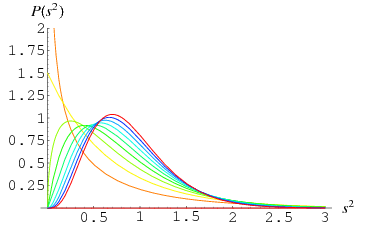
where 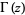 is the gamma function--a conjecture that was subsequently proven by R. A. Fisher. Curves are illustrated above for
is the gamma function--a conjecture that was subsequently proven by R. A. Fisher. Curves are illustrated above for 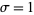 and
and 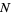 varying from
varying from 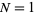 to 10.
to 10.
REFERENCES:
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Rose, C. and Smith, M. D. Mathematical Statistics with Mathematica. New York: Springer-Verlag, 2002.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|