


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-3-2021
Date: 16-2-2021
Date: 1-5-2021
|
The Lorenz asymmetry coefficient is a summary statistic of the Lorenz curve that measures the degree of asymmetry of a Lorenz curve. The Lorenz asymmetry coefficient is defined as
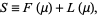 |
(1) |
where the functions 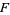 and
and 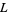 are defined as for the Lorenz curve. If
are defined as for the Lorenz curve. If 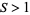 , then the point where the Lorenz curve is parallel with the line of equality is above the axis of symmetry. Correspondingly, if
, then the point where the Lorenz curve is parallel with the line of equality is above the axis of symmetry. Correspondingly, if 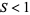 , then the point where the Lorenz curve is parallel to the line of equality is below the axis of symmetry.
, then the point where the Lorenz curve is parallel to the line of equality is below the axis of symmetry.
The sample statistic 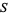 can be calculated from ordered size data using the following equations
can be calculated from ordered size data using the following equations
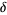 |
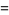 |
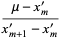 |
(2) |
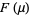 |
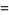 |
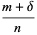 |
(3) |
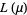 |
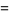 |
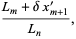 |
(4) |
where 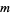 is the number of individuals with a size less than
is the number of individuals with a size less than 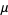 .
.
REFERENCES:
Damgaard, C. and Weiner, J. "Describing Inequality in Plant Size or Fecundity." Ecology 81, 1139-1142, 2000.a



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم الشؤون الفكرية ينظم ندوة ثقافية بذكرى فاجعة هدم قبور أئمة البقيع (عليهم السلام)
|
|
|