


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-9-2020
Date: 28-10-2019
Date: 19-1-2020
|
A McNugget number is a positive integer that can be obtained by adding together orders of McDonald's® Chicken McNuggetsTM (prior to consuming any), which originally came in boxes of 6, 9, and 20 (Vardi 1991, pp. 19-20 and 233-234; Wah and Picciotto 1994, p. 186). All integers are McNugget numbers except 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, and 43. The value 43 therefore corresponds to the Frobenius number of 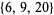 .
.
Since the Happy MealTM-sized nugget box (4 to a box) can now be purchased separately, the modern McNugget numbers are linear combinations of 4, 6, 9, and 20. These new-fangled numbers are much less interesting than before, with only 1, 2, 3, 5, 7, and 11 remaining as non-McNugget numbers. The value 11 therefore corresponds to the Frobenius number of 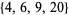 .
.
The greedy algorithm can be used to find a McNugget expansion of a given integer 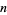 . This can also be done in the Wolfram Language using FrobeniusSolve[
. This can also be done in the Wolfram Language using FrobeniusSolve[ 6, 9, 20
6, 9, 20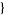 , n]. The following table summarizes (classic) McNugget expansions for small integers.
, n]. The following table summarizes (classic) McNugget expansions for small integers.
 |
McNugget expansions |
| 6 | 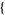 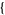 1,0,0 1,0,0  |
| 9 |   0,1,0 0,1,0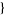 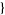 |
| 12 | 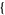 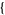 2,0,0 2,0,0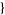 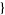 |
| 15 | 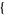 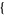 1,1,0 1,1,0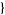 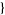 |
| 18 | 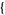 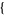 0,2,0 0,2,0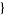 , ,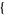 3,0,0 3,0,0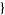 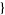 |
| 20 |   0,0,1 0,0,1  |
| 21 | 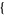 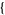 2,1,0 2,1,0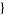 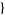 |
| 24 | 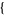 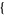 1,2,0 1,2,0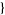 , ,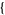 4,0,0 4,0,0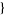 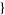 |
| 26 | 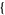 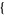 1,0,1 1,0,1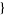 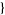 |
| 27 | 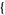 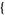 0,3,0 0,3,0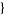 , , 3,1,0 3,1,0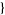  |
| 29 | 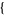 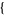 0,1,1 0,1,1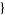 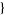 |
| 30 | 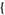 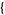 2,2,0 2,2,0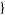 , ,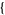 5,0,0 5,0,0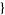 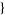 |
REFERENCES:
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 19-20 and 233-234, 1991.
Wagon, S. "Greedy Coins." https://library.wolfram.com/infocenter/MathSource/5187/.
Wah, A. and Picciotto, H. Lesson 5.8, Problem 1 in Algebra Themes, Tools and Concepts. Mountain View, CA: Creative Publications, p. 186, 1994.
Wilson, D. rec.puzzles newsgroup posting, March 20, 1990.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|