


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-12-2020
Date: 30-9-2020
Date: 16-9-2020
|
A number which is simultaneously square and triangular. Let 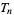 denote the
denote the 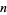 th triangular number and
th triangular number and 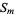 the
the 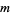 th square number, then a number which is both triangular and square satisfies the equation
th square number, then a number which is both triangular and square satisfies the equation 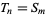 , or
, or
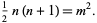 |
(1) |
Completing the square gives
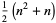 |
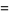 |
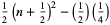 |
(2) |
 |
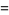 |
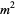 |
(3) |
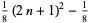 |
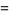 |
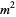 |
(4) |
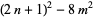 |
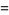 |
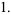 |
(5) |
Therefore, defining
 |
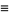 |
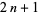 |
(6) |
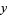 |
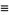 |
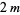 |
(7) |
gives the Pell equation
 |
(8) |
(Conway and Guy 1996). The first few solutions are 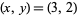 , (17, 12), (99, 70), (577, 408), .... These give the solutions
, (17, 12), (99, 70), (577, 408), .... These give the solutions 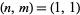 , (8, 6), (49, 35), (288, 204), ... (OEIS A001108 and A001109), corresponding to the triangular square numbers 1, 36, 1225, 41616, 1413721, 48024900, ... (OEIS A001110; Pietenpol 1962). In 1730, Euler showed that there are an infinite number of such solutions (Dickson 2005).
, (8, 6), (49, 35), (288, 204), ... (OEIS A001108 and A001109), corresponding to the triangular square numbers 1, 36, 1225, 41616, 1413721, 48024900, ... (OEIS A001110; Pietenpol 1962). In 1730, Euler showed that there are an infinite number of such solutions (Dickson 2005).
The general formula for a square triangular number 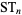 is
is 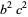 , where
, where 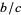 is the
is the 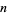 th convergent to the continued fraction of
th convergent to the continued fraction of 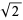 (Ball and Coxeter 1987, p. 59; Conway and Guy 1996). The first few are
(Ball and Coxeter 1987, p. 59; Conway and Guy 1996). The first few are
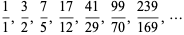 |
(9) |
(OEIS A001333 and A000129). The numerators and denominators can also be obtained by doubling the previous fraction and adding to the fraction before that.
A general formula for square triangular numbers is
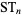 |
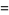 |
![[((1+sqrt(2))^(2n)-(1-sqrt(2))^(2n))/(4sqrt(2))]^2](https://mathworld.wolfram.com/images/equations/SquareTriangularNumber/Inline33.gif) |
(10) |
 |
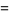 |
![1/(32)[(17+12sqrt(2))^n+(17-12sqrt(2))^n-2].](https://mathworld.wolfram.com/images/equations/SquareTriangularNumber/Inline36.gif) |
(11) |
The square triangular numbers also satisfy the recurrence relation
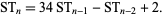 |
(12) |
A second-order recurrence for 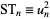 is given by
is given by
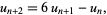 |
(13) |
with 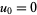 and
and 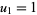 . A first-order recurrence equation is given by
. A first-order recurrence equation is given by
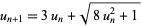 |
(14) |
(M. Carreira, pers. comm., Sept. 29, 2003).
A curious product formula for 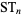 is given by
is given by
![ST_n=2^(2n-5)product_(k=1)^(2n)[3+cos((kpi)/n)].](https://mathworld.wolfram.com/images/equations/SquareTriangularNumber/NumberedEquation7.gif) |
(15) |
An amazing generating function is
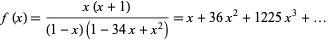 |
(16) |
(Sloane and Plouffe 1995).
Taking the square and triangular numbers together gives the sequence 1, 1, 3, 4, 6, 9, 10, 15, 16, 21, 25, ... (OEIS A005214; Hofstadter 1996, p. 15).
REFERENCES:
Allen, B. M. "Squares as Triangular Numbers." Scripta Math. 20, 213-214, 1954.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, 1987.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 203-205, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 10, 16, and 27, 2005.
Guy, R. K. "Sums of Squares" and "Figurate Numbers." §C20 and §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138 and 147-150, 1994.
Hofstadter, D. R. Fluid Concepts & Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought. New York: Basic Books, 1996.
Khatri, M. N. "Triangular Numbers Which are Also Squares." Math. Student 27, 55-56, 1959.
Pietenpol, J. L. "Square Triangular Numbers." Problem E 1473. Amer. Math. Monthly 69, 168-169, 1962.
Potter, D. C. D. "Triangular Square Numbers." Math. Gaz. 56, 109-110, 1972.
Sengupta, D. "Digits in Triangular Squares." College Math. J. 30, 31, 1999.
Sierpiński, W. Teoria Liczb, 3rd ed. Warsaw, Poland: Monografie Matematyczne t. 19, p. 517, 1950.
Sierpiński, W. "Sur les nombres triangulaires carrés." Pub. Faculté d'Électrotechnique l'Université Belgrade, No. 65, 1-4, 1961.
Sierpiński, W. "Sur les nombres triangulaires carrés." Bull. Soc. Royale Sciences Liège, 30 ann., 189-194, 1961.
Silverman, J. H. A Friendly Introduction to Number Theory. Englewood Cliffs, NJ: Prentice Hall, 1996.
Sloane, N. J. A. Sequences A000129/M1413, A001333/M2665, A001108/M4536, A001109/M4217, and A001110/M5259 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Walker, G. W. "Triangular Squares." Problem E 954. Amer. Math. Monthly 58, 568, 1951.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|