Square-Triangle Theorem

The square-triangle theorem states that any nonnegative integer can be represented as the sum of a square, an even square, and a triangular number (Sun 2005), i.e.,

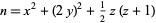(1)

for , , 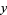and 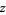 integers. For example,

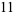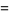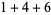			(2)
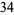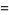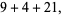			(3)

corresponding to the solutions 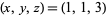 and (3,1,6), respectively.

Values of 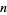 lacking a representation in which all of , , 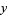and 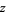 all are nonzero are 1, 2, 3, 4, 7, 10, 12, 22, and 24 (OEIS A118426).

The following table gives solutions for the first few .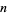

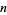	solutions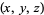
1	, , , , ,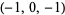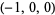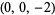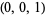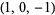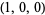
2	, , ,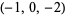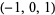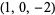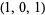
3	,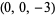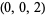
4	, , , , , , , , ,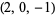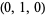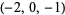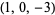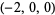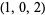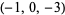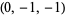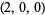
5	, , , , , , , , ,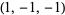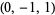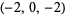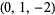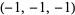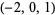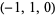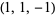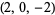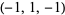
6	, , , , , , , , ,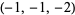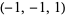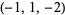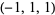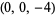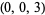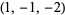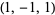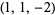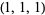
7	, , , , , , , , ,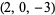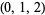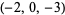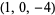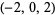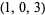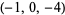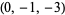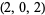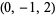
8	, , , , , , , , ,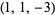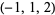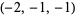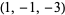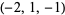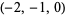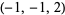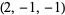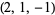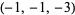
9	, , , , , , , , ,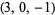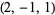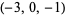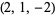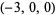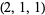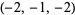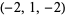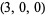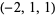
10	, , , , , , , , ,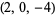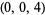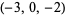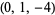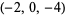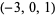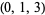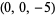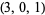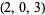

The numbers of solutions for 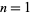, 2, ... are 6, 4, 2, 12, 16, 10, 12, 16, 12, 14, 20, 4, 8, 24, 14, ... (OEIS A118421). The high-water marks are 6, 12, 16, 20, 24, 28, 32, 40, 44, 56, 60, 72, 80, 88, 96, 108, ... (OEIS A118422), which occur for 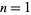, 4, 5, 11, 14, 19, 20, 23, 26, 41, 53, 68, 86, 110, 145, ... (OEIS A118423).

REFERENCES:

Sloane, N. J. A. Sequences A118421, A118422, A118422, and A118426 in "The On-Line Encyclopedia of Integer Sequences."

Sun, Z.-W. "Each Natural Number is of the Form 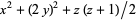." 9 May 2005. https://arxiv.org/abs/math/0505128.