


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2020
Date: 10-2-2020
Date: 31-8-2020
|
A number 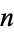 is called
is called 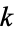 -hyperperfect if
-hyperperfect if
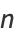 |
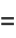 |
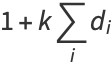 |
(1) |
 |
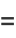 |
![1+k[sigma(n)-n-1],](https://mathworld.wolfram.com/images/equations/HyperperfectNumber/Inline8.gif) |
(2) |
where 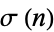 is the divisor function and the summation is over the proper divisors with
is the divisor function and the summation is over the proper divisors with 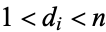 . Rearranging gives
. Rearranging gives
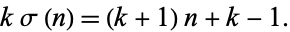 |
(3) |
Taking 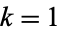 gives the usual perfect numbers.
gives the usual perfect numbers.
If 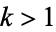 is an odd integer, and
is an odd integer, and 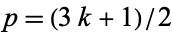 and
and 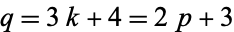 are prime, then
are prime, then 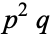 is
is 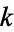 -hyperperfect. McCranie (2000) conjectures that all
-hyperperfect. McCranie (2000) conjectures that all 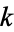 -hyperperfect numbers for odd
-hyperperfect numbers for odd 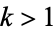 are in fact of this form. Similarly, if
are in fact of this form. Similarly, if 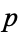 and
and 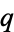 are distinct odd primes such that
are distinct odd primes such that 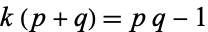 for some integer
for some integer 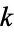 , then
, then 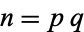 is
is 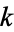 -hyperperfect. Finally, if
-hyperperfect. Finally, if 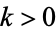 and
and 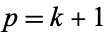 is prime, then if
is prime, then if 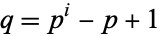 is prime for some
is prime for some 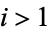 < then
< then 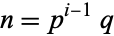 is
is 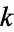 -hyperperfect (McCranie 2000).
-hyperperfect (McCranie 2000).
The first few hyperperfect numbers (excluding perfect numbers) are 21, 301, 325, 697, 1333, ... (OEIS A007592). If perfect numbers are included, the first few are 6, 21, 28, 301, 325, 496, ... (OEIS A034897), whose corresponding values of 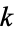 are 1, 2, 1, 6, 3, 1, 12, ... (OEIS A034898). The following table gives the first few
are 1, 2, 1, 6, 3, 1, 12, ... (OEIS A034898). The following table gives the first few 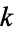 -hyperperfect numbers for small values of
-hyperperfect numbers for small values of 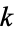 . McCranie (2000) has tabulated all hyperperfect numbers less than
. McCranie (2000) has tabulated all hyperperfect numbers less than 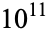 .
.
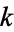 |
OEIS | 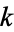 -hyperperfect number -hyperperfect number |
| 1 | A000396 | 6 ,28, 496, 8128, ... |
| 2 | A007593 | 21, 2133, 19521, 176661, ... |
| 3 | 325, ... | |
| 4 | 1950625, 1220640625, ... | |
| 6 | A028499 | 301, 16513, 60110701, ... |
| 10 | 159841, ... | |
| 11 | 10693, ... | |
| 12 | A028500 | 697, 2041, 1570153, 62722153, ... |
REFERENCES:
Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.
McCranie, J. S. "A Study of Hyperperfect Numbers." J. Integer Sequences 3, No. 00.1.3, 2000. https://www.math.uwaterloo.ca/JIS/VOL3/VOL3/mccranie.
Minoli, D. "Issues in Nonlinear Hyperperfect Numbers." Math. Comput. 34, 639-645, 1980.
Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., p. 177, 1992.
Sloane, N. J. A. Sequences A000396/M4186, A007592/M5113, A007593/M5121, A028499, A028500, A034897, and A034898 in "The On-Line Encyclopedia of Integer Sequences."
te Riele, H. J. J. "Hyperperfect Numbers with Three Different Prime Factors." Math. Comput. 36, 297-298, 1981.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|