Reversal

The reversal of a positive integer 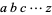 is 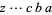. The reversal of a positive integer  is implemented in the Wolfram Language as IntegerReverse[n].

A positive integer that is the same as its own reversal is known as a palindromic number.

Ball and Coxeter (1987) consider numbers whose reversals are integral multiples of themselves. Palindromic numbers and numbers ending with a zero are trivial examples.

The first few nontrivial examples of numbers whose reversals are multiples of themselves are 8712, 9801, 87912, 98901, 879912, 989901, 8799912, 9899901, 87128712, 87999912, 98019801, 98999901, ... (OEIS A031877). The pattern continues for large numbers, with numbers of the form 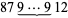 equal to 4 times their reversals and numbers of the form  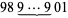equal to 9 times their reversals. In addition, runs of numbers of either of these forms can be concatenated to yield numbers of the form 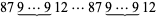, equal to 4 times their reversals, and 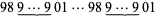, equal to 9 times their reversals.

The reversals corresponding to the above are 1089, 2178, 10989, 21978, 109989, 219978, ... (OEIS A008919).

The product of a 2-digit number and its reversal is never a square number except when the digits are the same (Ogilvy 1988).

Numbers whose product is the reversal of the products of their reversals include (221, 312) and (122, 213), since

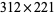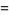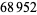			(1)
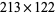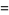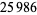			(2)

(Ball and Coxeter 1987, p. 14).

Non-palindromic numbers 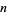 such that  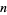is not divisible by 10 and  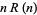is square, where  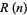is the reversal of 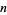, are given by 144, 169, 288, 441, 528, ... (OEIS A062917).

The only known powers greater than squared resulting from reversal multiplication are

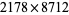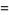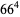			(3)
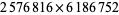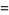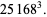			(4)

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 14-15, 1987.

Edalj, J. Problem 1622. L'Interméd. Math. 16, 34, 1909.

Jonesco, J. Problem 1622. L'Interméd. Math. 15, 128, 1908.

Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, pp. 88-89, 1988.

Sloane, N. J. A. Sequences A008919, A031877, and A062917 in "The On-Line Encyclopedia of Integer Sequences."

Welsch. Problem 1622. L'Interméd. Math. 15, 278, 1908.