


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-9-2020
Date: 29-12-2019
Date: 11-10-2020
|
If 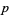 and
and 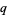 are distinct odd primes, then the quadratic reciprocity theorem states that the congruences
are distinct odd primes, then the quadratic reciprocity theorem states that the congruences
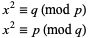 |
(1) |
are both solvable or both unsolvable unless both 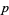 and
and 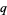 leave the remainder 3 when divided by 4 (in which case one of the congruences is solvable and the other is not). Written symbolically,
leave the remainder 3 when divided by 4 (in which case one of the congruences is solvable and the other is not). Written symbolically,
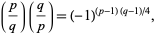 |
(2) |
where
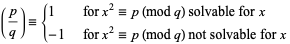 |
(3) |
is known as a Legendre symbol.
Gauss called this result the "aureum theorema" (golden theorem).
Euler stated the theorem in 1783 without proof. Legendre was the first to publish a proof, but it was fallacious. In 1796, Gauss became the first to publish a correct proof (Nagell 1951, p. 144). The quadratic reciprocity theorem was Gauss's favorite theorem from number theory, and he devised no fewer than eight different proofs of it over his lifetime.
The genus theorem states that the Diophantine equation
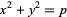 |
(4) |
can be solved for 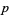 a prime iff
a prime iff 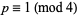 or
or  .
.
REFERENCES:
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 39, 1996.
Ireland, K. and Rosen, M. "Quadratic Reciprocity." Ch. 5 in A Classical Introduction to Modern Number Theory, 2nd ed. New York:Springer-Verlag, pp. 50-65, 1990.
Jones, G. A. and Jones, J. M. "Quadratic Reciprocity." §7.4 in Elementary Number Theory. Berlin:Springer-Verlag, pp. 130-135, 1998.
Nagell, T. "The Quadratic Reciprocity Law." §41 in Introduction to Number Theory. New York: Wiley, pp. 141-145, 1951.
Riesel, H. "The Law of Quadratic Reciprocity." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 279-281, 1994.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 42-49, 1993.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
قسم رعاية الصحن ينهي أعماله الخاصة بإقامة الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|