


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-12-2020
Date: 25-12-2020
Date: 25-12-2020
|
If there is no integer 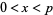 such that
such that
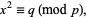 |
i.e., if the congruence (35) has no solution, then 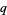 is said to be a quadratic nonresidue (mod
is said to be a quadratic nonresidue (mod 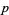 ). If the congruence (35) does have a solution, then
). If the congruence (35) does have a solution, then 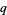 is said to be a quadratic residue (mod
is said to be a quadratic residue (mod 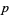 ).
).
In practice, it suffices to restrict the range to 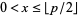 , where
, where 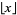 is the floor function, because of the symmetry
is the floor function, because of the symmetry 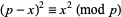 .
.

The following table summarizes the quadratic nonresidues for small 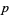 (OEIS A105640).
(OEIS A105640).
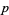 |
quadratic nonresidues |
| 1 | (none) |
| 2 | (none) |
| 3 | 2 |
| 4 | 2, 3 |
| 5 | 2, 3 |
| 6 | 2, 5 |
| 7 | 3, 5, 6 |
| 8 | 2, 3, 5, 6, 7 |
| 9 | 2, 3, 5, 6, 8 |
| 10 | 2, 3, 7, 8 |
| 11 | 2, 6, 7, 8, 10 |
| 12 | 2, 3, 5, 6, 7, 8, 10, 11 |
| 13 | 2, 5, 6, 7, 8, 11 |
| 14 | 3, 5, 6, 10, 12, 13 |
| 15 | 2, 3, 5, 7, 8, 11, 12, 13, 14 |
| 16 | 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 |
| 17 | 3, 5, 6, 7, 10, 11, 12, 14 |
| 18 | 2, 3, 5, 6, 8, 11, 12, 14, 15, 17 |
| 19 | 2, 3, 8, 10, 12, 13, 14, 15, 18 |
| 20 | 2, 3, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19 |
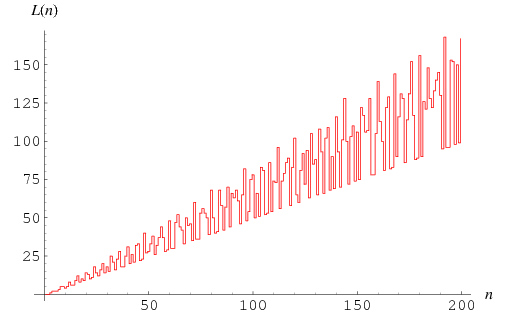
The numbers of quadratic nonresidues (mod 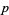 ) for
) for 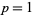 , 2, ... are 0, 0, 1, 2, 2, 2, 3, 5, 5, 4, 5, 8, 6, 6, ... (OEIS A095972).
, 2, ... are 0, 0, 1, 2, 2, 2, 3, 5, 5, 4, 5, 8, 6, 6, ... (OEIS A095972).
The smallest quadratic nonresidues for 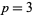 , 4, ... are 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 2, 3, 2, 2, 3, 2, 2, ... (OEIS A020649). The smallest quadratic nonresidues for
, 4, ... are 2, 2, 2, 2, 3, 2, 2, 2, 2, 2, 2, 3, 2, 2, 3, 2, 2, ... (OEIS A020649). The smallest quadratic nonresidues for 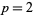 , 3, 5, 7, 11, ... are 2, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 3, ... (OEIS A053760).
, 3, 5, 7, 11, ... are 2, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 3, ... (OEIS A053760).
If the extended Riemann hypothesis is true, then the first quadratic nonresidue of a number (mod 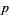 ) is always less than
) is always less than 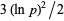 (Wedeniwski 2001) for
(Wedeniwski 2001) for 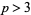 .
.
The following table gives the values of 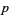 such that the least quadratic nonresidue is
such that the least quadratic nonresidue is 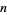 for small
for small 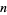 .
.
 |
OEIS | 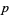 such that such that 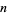 is the smallest quadratic nonresidue is the smallest quadratic nonresidue |
| 2 | A025020 | 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 15, ... |
| 3 | A025021 | 7, 14, 17, 31, 34, 41, 49, 62, 79, 82, ... |
| 5 | A025022 | 23, 46, 47, 73, 94, 97, 146, 167, 193, ... |
| 7 | A025023 | 71, 142, 191, 239, 241, 359, 382, ... |
REFERENCES:
Sloane, N. J. A. Sequences A020649, A025020, A025021, A025022, A025023, A053760, A095972, and A105640 in "The On-Line Encyclopedia of Integer Sequences."
Wedeniwski, S. "Primality Tests on Commutator Curves." Dissertation. Tübingen, Germany, 2001. https://www.hipilib.de/prime/primality-tests-on-commutator-curves.pdf.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|