Giuga Number

Any composite number 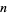 with 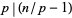 for all prime divisors  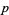of 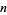.  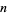is a Giuga number iff

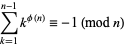(1)

where 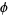 is the totient function and iff

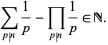(2)

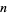 is a Giuga number iff

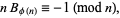(3)

where 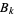 is a Bernoulli number and  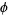is the totient function. Every counterexample to Giuga's conjecture is a contradiction to Agoh's conjecture and vice versa. The smallest known Giuga numbers are 30 (3 factors), 858, 1722 (4 factors), 66198 (5 factors), 2214408306, 24423128562 (6 factors), 432749205173838, 14737133470010574, 550843391309130318 (7 factors),

244197000982499715087866346, 554079914617070801288578559178

(8 factors), ... (OEIS A007850).

It is not known if there are an infinite number of Giuga numbers. All the above numbers have sum minus product equal to 1, and any Giuga number of higher order must have at least 59 factors. The smallest odd Giuga number must have at least nine prime factors.

REFERENCES:

Borwein, D.; Borwein, J. M.; Borwein, P. B.; and Girgensohn, R. "Giuga's Conjecture on Primality." Amer. Math. Monthly 103, 40-50, 1996.

Butske, W.; Jaje, L. M.; and Mayernik, D. R. "The Equation 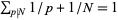, Pseudoperfect Numbers, and Partially Weighted Graphs." Math. Comput. 69, 407-420, 1999.

Kellner, B. C. Über irreguläre Paare höherer Ordnungen. Diplomarbeit. Göttingen, Germany: Mathematischen Institut der Georg August Universität zu Göttingen, 2002. https://www.bernoulli.org/~bk/irrpairord.pdf.

Kellner, B. C. "The Equivalence of Giuga's and Agoh's Conjectures." Preprint. 10 July 2003. https://www.bernoulli.org/~bk/equivalence.pdf.

Sloane, N. J. A. Sequence A007850 in "The On-Line Encyclopedia of Integer Sequences."