المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Feller-Tornier Constant |
 514
 03:47 مساءً
date: 3-10-2020 |
Author : Cohen, E. 
Book or Source : "Some Asymptotic Formulas in the Theory of Numbers." Trans. Amer. Math. Soc. 112 
Page and Part : ...|
Read More
Date: 16-12-2020
733
Date: 9-3-2020
1711
Date: 28-11-2020
803
|
The Feller-Tornier constant is the density of integers that have an even number of prime factors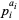 
with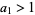 
in their prime factorization. It is given by
 |
 |
 |
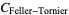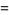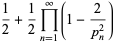(1) |
 |
 |
 |
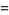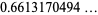(2) |
(OEIS A065493), where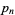 
is the 
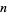th prime. It can be given by the sum
![C_(Feller-Tornier)=1/2{1+exp[-sum_(n=1)^infty(2^nP(n))/n]},](https://mathworld.wolfram.com/images/equations/Feller-TornierConstant/NumberedEquation1.gif) |
(3) |
where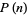 
is the prime zeta function.
REFERENCES:
Cohen, E. "Some Asymptotic Formulas in the Theory of Numbers." Trans. Amer. Math. Soc. 112, 214-227, 1964.
Feller, W. and Tornier, E. "Mengentheoretische Untersuchungen von Eigenschaften der Zahlenreihe." Math. Ann. 107, 188-232, 1933.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 106, 2003.
Niklasch, G. "Some Number-Theoretical Constants." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Schoenberg, I. J. "On Asymptotic Distributions of Arithmetical Functions." Trans. Amer. Math. Soc. 39, 315-330, 1936.
Sloane, N. J. A. Sequence A065493 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
