


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-12-2020
Date: 31-1-2020
Date: 14-3-2020
|
If 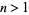 and
and
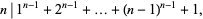 |
is 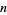 necessarily a prime? In other words, defining
necessarily a prime? In other words, defining
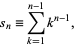 |
does there exist a composite 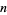 such that
such that 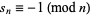 ? It is known that
? It is known that 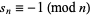 iff for each prime divisor
iff for each prime divisor 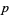 of
of 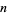 ,
, 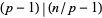 and
and 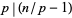 (Giuga 1950, Borwein et al. 1996); therefore, any counterexample must be squarefree. A composite integer
(Giuga 1950, Borwein et al. 1996); therefore, any counterexample must be squarefree. A composite integer 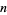 satisfies
satisfies 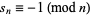 iff it is both a Carmichael number and a Giuga number. Giuga showed that there are no exceptions to the conjecture up to
iff it is both a Carmichael number and a Giuga number. Giuga showed that there are no exceptions to the conjecture up to 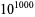 . This was later improved to
. This was later improved to 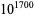 (Bedocchi 1985) and
(Bedocchi 1985) and 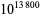 (Borwein et al. 1996).
(Borwein et al. 1996).
Kellner (2002) provided a short proof of the equivalence of Giuga's and Agoh's conjectures. The combined conjecture can be described by a sum of fractions.
REFERENCES:
Bedocchi, E. "The 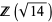 Ring and the Euclidean Algorithm." Manuscripta Math. 53, 199-216, 1985.
Ring and the Euclidean Algorithm." Manuscripta Math. 53, 199-216, 1985.
Borwein, D.; Borwein, J. M.; Borwein, P. B.; and Girgensohn, R. "Giuga's Conjecture on Primality." Amer. Math. Monthly 103, 40-50, 1996.
Giuga, G. "Su una presumibile propertietà caratteristica dei numeri primi." Ist. Lombardo Sci. Lett. Rend. A 83, 511-528, 1950.
Kellner, B. C. Über irreguläre Paare höherer Ordnungen. Diplomarbeit. Göttingen, Germany: Mathematischen Institut der Georg August Universität zu Göttingen, 2002. https://www.bernoulli.org/~bk/irrpairord.pdf.
Kellner, B. C. "The Equivalence of Giuga's and Agoh's Conjectures." 15 Sep 2004. https://arxiv.org/abs/math.NT/0409259.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 20-21, 1989.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|