


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-2-2021
Date: 23-11-2019
Date: 12-3-2020
|
A prime constellation, also called a prime 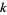 -tuple, prime
-tuple, prime 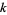 -tuplet, or prime cluster, is a sequence of
-tuplet, or prime cluster, is a sequence of 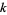 consecutive numbers such that the difference between the first and last is, in some sense, the least possible. More precisely, a prime
consecutive numbers such that the difference between the first and last is, in some sense, the least possible. More precisely, a prime 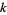 -tuplet is a sequence of consecutive primes (
-tuplet is a sequence of consecutive primes (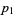 ,
, 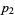 , ...,
, ..., 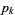 ) with
) with 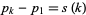 , where
, where 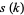 is the smallest number
is the smallest number 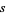 for which there exist
for which there exist 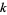 integers
integers 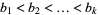 ,
, 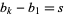 and, for every prime
and, for every prime 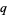 , not all the residues modulo
, not all the residues modulo 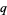 are represented by
are represented by 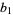 ,
, 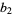 , ...,
, ..., 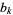 (Forbes). For each
(Forbes). For each 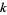 , this definition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101, 103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not because all three residues modulo 3 are represented (Forbes).
, this definition excludes a finite number of clusters at the beginning of the prime number sequence. For example, (97, 101, 103, 107, 109) satisfies the conditions of the definition of a prime 5-tuplet, but (3, 5, 7, 11, 13) does not because all three residues modulo 3 are represented (Forbes).
A prime double with 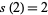 is of the form (
is of the form (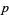 ,
, 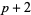 ) and is called a pair of twin primes. Prime doubles of the form (
) and is called a pair of twin primes. Prime doubles of the form (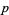 ,
, 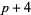 ) are called cousin primes, and prime doubles of the form (
) are called cousin primes, and prime doubles of the form (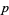 ,
, 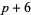 ) are called sexy primes.
) are called sexy primes.
A prime triplet has 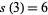 . The constellation (
. The constellation (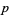 ,
, 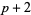 ,
, 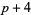 ) cannot exist, except for
) cannot exist, except for 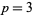 , since one of
, since one of 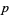 ,
, 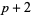 , and
, and 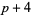 must be divisible by three. However, there are several types of prime triplets which can exist: (
must be divisible by three. However, there are several types of prime triplets which can exist: (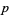 ,
, 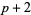 ,
, 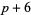 ), (
), (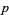 ,
, 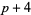 ,
, 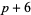 ), (
), (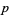 ,
, 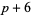 ,
, 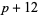 ).
).
A prime quadruplet is a constellation of four successive primes with minimal distance 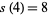 , and is of the form (
, and is of the form (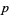 ,
, 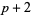 ,
, 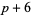 ,
, 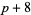 ). The sequence
). The sequence 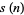 therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (OEIS A008407). Another quadruplet constellation is (
therefore begins 2, 6, 8, and continues 12, 16, 20, 26, 30, ... (OEIS A008407). Another quadruplet constellation is (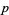 ,
, 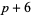 ,
, 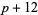 ,
, 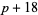 ).
).
Hardy and Wright (1979, p. 5) conjecture, and it seems almost certain to be true, that there are infinitely many twin primes (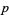 ,
, 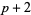 ) and prime triplets of the form (
) and prime triplets of the form (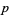 ,
, 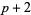 ,
, 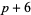 ) and (
) and (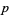 ,
, 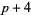 ,
, 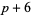 ).
).
The first Hardy-Littlewood conjecture states that the numbers of constellations 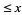 are asymptotically given by
are asymptotically given by
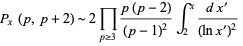 |
(1) |
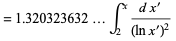 |
(2) |
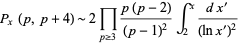 |
(3) |
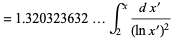 |
(4) |
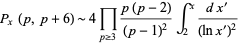 |
(5) |
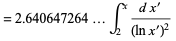 |
(6) |
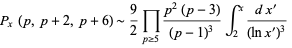 |
(7) |
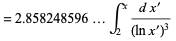 |
(8) |
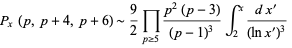 |
(9) |
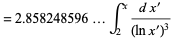 |
(10) |
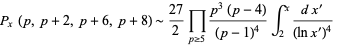 |
(11) |
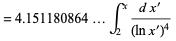 |
(12) |
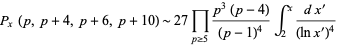 |
(13) |
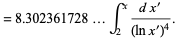 |
(14) |
These numbers are sometimes called the Hardy-Littlewood constants, and are OEIS A114907, ....
(◇) is sometimes called the extended twin prime conjecture, and
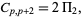 |
(15) |
where 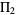 is the twin primes constant. Riesel (1994) remarks that the Hardy-Littlewood constants can be computed to arbitrary accuracy without needing the infinite sequence of primes.
is the twin primes constant. Riesel (1994) remarks that the Hardy-Littlewood constants can be computed to arbitrary accuracy without needing the infinite sequence of primes.
The integrals above have the analytic forms
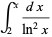 |
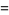 |
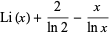 |
(16) |
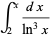 |
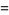 |
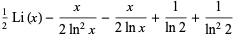 |
(17) |
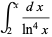 |
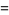 |
![[(Li(x))/6-x/(3ln^3x)-x/(6ln^2x)-x/(6lnx)+2/(3ln^32)+1/(3ln^22)+1/(3ln2)],](https://mathworld.wolfram.com/images/equations/PrimeConstellation/Inline86.gif) |
(18) |
where 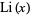 is the logarithmic integral.
is the logarithmic integral.
The following table gives the number of prime constellations 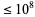 , and the second table gives the values predicted by the Hardy-Littlewood formulas.
, and the second table gives the values predicted by the Hardy-Littlewood formulas.
| count | 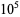 |
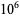 |
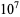 |
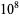 |
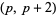 |
1224 | 8169 | 58980 | 440312 |
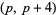 |
1216 | 8144 | 58622 | 440258 |
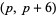 |
2447 | 16386 | 117207 | 879908 |
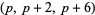 |
259 | 1393 | 8543 | 55600 |
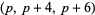 |
248 | 1444 | 8677 | 55556 |
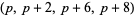 |
38 | 166 | 899 | 4768 |
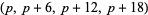 |
75 | 325 | 1695 | 9330 |
| Hardy-Littlewood | 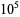 |
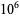 |
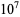 |
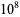 |
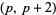 |
1249 | 8248 | 58754 | 440368 |
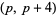 |
1249 | 8248 | 58754 | 440368 |
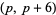 |
2497 | 16496 | 117508 | 880736 |
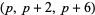 |
279 | 1446 | 8591 | 55491 |
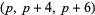 |
279 | 1446 | 8591 | 55491 |
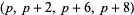 |
53 | 184 | 863 | 4735 |
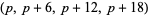 |
Consider prime constellations in which each term is of the form 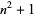 . Hardy and Littlewood showed that the number of prime constellations of this form
. Hardy and Littlewood showed that the number of prime constellations of this form 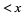 is given by
is given by
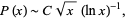 |
(19) |
where
![C=product_(p>2; p prime)[1-((-1)^((p-1)/2))/(p-1)]=1.3727...](https://mathworld.wolfram.com/images/equations/PrimeConstellation/NumberedEquation3.gif) |
(20) |
(Le Lionnais 1983).
Forbes gives a list of the "top ten" prime 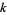 -tuples for
-tuples for 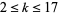 . The largest known 14-constellations are (
. The largest known 14-constellations are (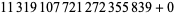 , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (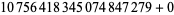 , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (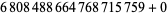 , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (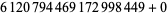 , 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (
, 2, 8, 14, 18, 20, 24, 30, 32, 38, 42, 44, 48, 50), (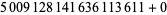 , 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
, 2, 6, 8, 12, 18, 20, 26, 30, 32, 36, 42, 48, 50).
The largest known prime 15-constellations are (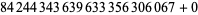 , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56), (
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56), (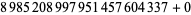 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (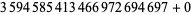 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (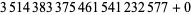 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56), (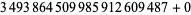 , 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
, 2, 6, 12, 14, 20, 24, 26, 30, 36, 42, 44, 50, 54, 56).
The largest known prime 16-constellations are (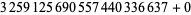 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (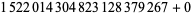 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (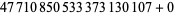 , 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
, 2, 6, 12, 14, 20, 26, 30, 32, 36, 42, 44, 50, 54, 56, 60), (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73).
The largest known prime 17-constellations are (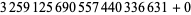 , 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66), (17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83) (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
, 6, 8, 12, 18, 20, 26, 32, 36, 38, 42, 48, 50, 56, 60, 62, 66), (17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83) (13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79).
Smith (1957) found 8 consecutive primes spaced like the cluster 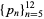 (Gardner 1980). K. Conrow and J. J. Devore have found 15 consecutive primes spaced like the cluster
(Gardner 1980). K. Conrow and J. J. Devore have found 15 consecutive primes spaced like the cluster 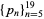 given by
given by 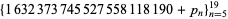 , the first member of which is 1632373745527558118201.
, the first member of which is 1632373745527558118201.
Rivera tabulates the smallest examples of 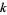 consecutive primes ending in a given digit
consecutive primes ending in a given digit 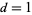 , 3, 7, or 9 for
, 3, 7, or 9 for 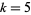 to 11. For example, 216401, 216421, 216431, 216451, 216481 is the smallest set of five consecutive primes ending in the digit 1.
to 11. For example, 216401, 216421, 216431, 216451, 216481 is the smallest set of five consecutive primes ending in the digit 1.
REFERENCES:
Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. https://www.math.u-bordeaux.fr/~cohen/hardylw.dvi.
Forbes, T. "Large Prime Quadruplets." 17 Sep 1998. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9809&L=nmbrthry&P=992.
Forbes, T. "Prime Clusters and Cunningham Chains." Math. Comput. 68, 1739-1748, 1999.
Forbes, T. "Prime 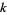 -Tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
-Tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
Gardner, M. "Mathematical Games." Sci. Amer. 243, Dec. 1980.
Guy, R. K. "Patterns of Primes." §A9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 23-25, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Rivera, C. "Problems & Puzzles: Puzzle 016-Consecutive Primes and Ending Digits." https://www.primepuzzles.net/puzzles/puzz_016.htm.
Smith, H. F. "On a Generalization of the Prime Pair Problem." Math. Tables Aids Comput. 11, 249-254, 1957.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 38, 1983.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 60-74, 1994.
Sloane, N. J. A. Sequences A008407 and A114907 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|