


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-12-2019
Date: 8-5-2020
Date: 28-10-2019
|
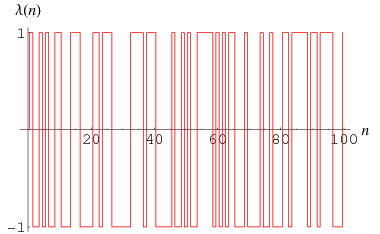
The function
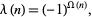 |
(1) |
where 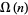 is the number of not necessarily distinct prime factors of
is the number of not necessarily distinct prime factors of  , with
, with 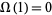 . The values of
. The values of 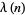 for
for 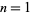 , 2, ... are 1,
, 2, ... are 1, 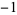 ,
, 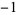 , 1,
, 1, 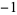 , 1,
, 1, 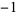 ,
, 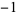 , 1, 1,
, 1, 1, 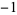 ,
, 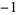 , ... (OEIS A008836). The values of
, ... (OEIS A008836). The values of 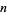 such that
such that 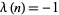 are 2, 3, 5, 7, 8, 11, 12, 13, 17, 18, 19, 20, 23, ... (OEIS A026424), while then values such that
are 2, 3, 5, 7, 8, 11, 12, 13, 17, 18, 19, 20, 23, ... (OEIS A026424), while then values such that 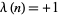 are 1, 4, 6, 9, 10, 14, 15, 16, 21, 22, 24, ... (OEIS A028260).
are 1, 4, 6, 9, 10, 14, 15, 16, 21, 22, 24, ... (OEIS A028260).
The Liouville function is implemented in the Wolfram Language as LiouvilleLambda[n].
The Liouville function is connected with the Riemann zeta function by the equation
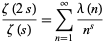 |
(2) |
(Lehman 1960). It has the Lambert series
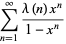 |
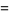 |
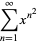 |
(3) |
 |
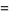 |
![1/2[theta_3(q)-1],](https://mathworld.wolfram.com/images/equations/LiouvilleFunction/Inline21.gif) |
(4) |
where 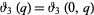 is a Jacobi theta function.
is a Jacobi theta function.
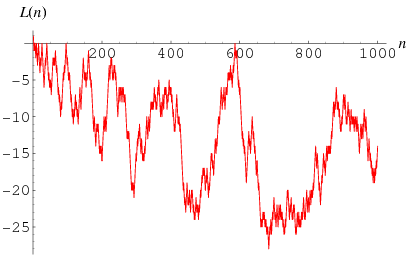
Consider the summatory function
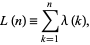 |
(5) |
the values of which for 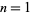 , 2, ... are 1, 0,
, 2, ... are 1, 0, 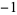 , 0,
, 0, 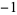 , 0,
, 0, 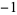 ,
, 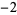 ,
, 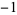 , 0,
, 0, 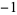 ,
, 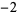 ,
, 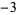 ,
, 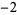 ,
, 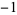 , 0,
, 0, 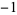 ,
, 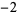 ,
, 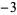 ,
, 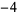 , ... (OEIS A002819).
, ... (OEIS A002819).
Lehman (1960) gives the formulas
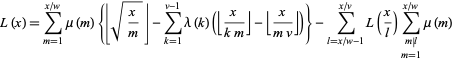 |
(6) |
and
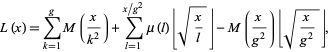 |
(7) |
where 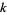 ,
, 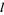 , and
, and 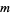 are variables ranging over the positive integers,
are variables ranging over the positive integers, 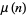 is the Möbius function,
is the Möbius function, 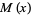 is Mertens function, and
is Mertens function, and 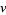 ,
, 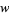 , and
, and  are positive real numbers with
are positive real numbers with 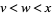 .
.
The conjecture that 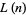 satisfies
satisfies 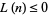 for
for 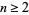 is called the Pólya conjecture and has been proved to be false.
is called the Pólya conjecture and has been proved to be false. 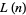 is positive for
is positive for 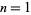 , but not for any other
, but not for any other 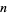 for a long time. In fact, the first
for a long time. In fact, the first 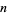 for which
for which 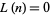 are for
are for 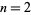 , 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (OEIS A028488), and
, 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (OEIS A028488), and 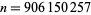 is the first counterexample to the Pólya conjecture (Tanaka 1980). However, it is unknown if
is the first counterexample to the Pólya conjecture (Tanaka 1980). However, it is unknown if 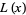 changes sign infinitely often (Tanaka 1980).
changes sign infinitely often (Tanaka 1980).
The values of 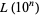 for
for 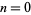 , 1, 2, ... are 1, 0,
, 1, 2, ... are 1, 0, 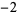 ,
, 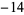 ,
, 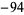 ,
, 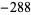 ,
, 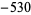 ,
, 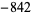 ,
, 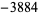 , ... (OEIS A090410).
, ... (OEIS A090410).
REFERENCES:
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, p. 37, 1976.
Fawaz, A. Y. "The Explicit Formula for 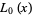 ." Proc. London Math. Soc. 1, 86-103, 1951.
." Proc. London Math. Soc. 1, 86-103, 1951.
Gupta, H. "On a Table of Values of 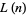 ." Proc. Indian Acad. Sci. Sec. A 12, 407-409, 1940.
." Proc. Indian Acad. Sci. Sec. A 12, 407-409, 1940.
Gupta, H. "A Table of Values of Liouville's Function 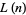 ." Res. Bull. East Panjab University, No. 3, 45-55, Feb. 1950.
." Res. Bull. East Panjab University, No. 3, 45-55, Feb. 1950.
Lehman, R. S. "On Liouville's Function." Math. Comput. 14, 311-320, 1960.
Ramanujan, S. "Irregular Numbers." J. Indian Math. Soc. 5, 105-106, 1913. Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., pp. 20-21, 2000.
Ribenboim, P. Algebraic Numbers. New York: Wiley, p. 44, 1972.
Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., p. 279, 1992.
Sloane, N. J. A. Sequences A002819/M0042, A008836, A026424, A028260, A028488, and A090410 in "The On-Line Encyclopedia of Integer Sequences."
Tanaka, M. "A Numerical Investigation on Cumulative Sum of the Liouville Function." Tokyo J. Math. 3, 187-189, 1980.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|