Strong Law of Large Numbers

The sequence of variates 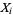 with corresponding means  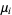obeys the strong law of large numbers if, to every pair 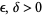, there corresponds an  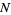such that there is probability  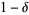or better that for every 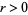, all 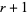 inequalities

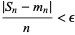(1)

for 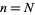, , 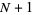...,  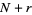will be satisfied, where

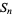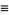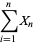			(2)
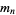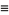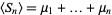			(3)

(Feller 1968). Kolmogorov established that the convergence of the sequence

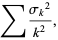(4)

sometimes called the Kolmogorov criterion, is a sufficient condition for the strong law of large numbers to apply to the sequence of mutually independent random variables 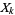 with variances  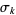(Feller 1968).

REFERENCES:

Feller, W. "The Strong Law of Large Numbers." §10.7 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 243-245, 1968.

Feller, W. "Strong Laws for Martingales." §7.8 in An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 234-238, 1971.