Irrationality Measure

Let  be a real number, and let 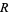 be the set of positive real numbers  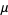for which

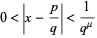(1)

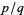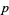has (at most) finitely many solutions  for  and 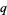 integers. Then the irrationality measure, sometimes called the Liouville-Roth constant or irrationality exponent, is defined as the threshold at which Liouville's approximation theorem kicks in and  is no longer approximable by rational numbers,

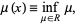(2)

where 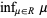 is the infimum. If the set  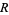is empty, then  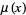is defined to be 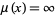, and  is called a Liouville number. There are three possible regimes for nonempty :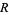

(3)

where the transitional case 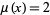 can correspond to  being either algebraic of degree 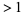 or  being transcendental. Showing that 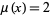 for  an algebraic number is a difficult result for which Roth was awarded the Fields medal.

The definition of irrationality measure is equivalent to the statement that if  has irrationality measure 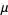, then  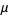is the smallest number such that the inequality

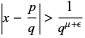(4)

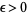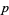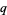holds for any  and all integers  and  with 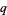 sufficiently large.

The irrationality measure of an irrational number  can be given in terms of its simple continued fraction expansion  and its convergent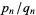s  as

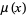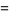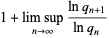			(5)
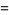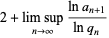			(6)

(Sondow 2004). For example, the golden ratio 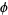 has

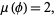(7)

which follows immediately from (6) and the simple continued fraction expansion .

Exact values include 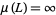 for 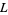 Liouville's constant and  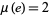(Borwein and Borwein 1987, pp. 364-365). The best known upper bounds for other common constants as of mid-2020 are summarized in the following table, where  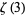is Apéry's constant,  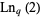and 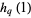 are q-harmonic series, and the lower bounds are 2.

constant	upper bound	reference
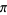	7.10320534	Zeilberger and Zudilin (2020)
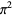	5.09541179	Zudilin (2103)
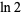	3.57455391	Marcovecchio (2009)
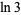	5.116201	Bondareva et al. (2018)
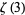	5.513891	Rhin and Viola (2001)
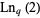	2.9384	Matala-Aho et al. (2006)
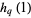	2.4650	Zudilin (2004)

The bound for 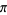 is due to Zeilberger and Zudilin (2020) and improves on the value 7.606308 previously found by Salikhov (2008). It has exact value given as follows. Let  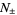be the complex conjugate roots of

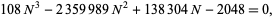(8)

let 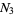 be the positive real root, and let

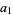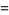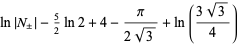			(9)
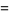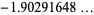			(10)
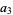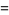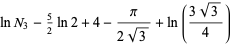			(11)
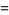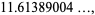			(12)

then the bound is given by

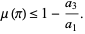(13)

Alekseyev (2011) has shown that the question of the convergence of the Flint Hills series is related to the irrationality measure of 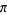, and in particular, convergence would imply 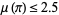, which is much stronger than the best currently known upper bound.

REFERENCES:

Alekseyev, M. A. "On Convergence of the Flint Hills Series." http://arxiv.org/abs/1104.5100/. 27 Apr 2011.

Amdeberhan, T. and Zeilberger, D. "q-Apéry Irrationality Proofs by q-WZ Pairs." Adv. Appl. Math. 20, 275-283, 1998.

Beukers, F. "A Rational Approach to Pi." Nieuw Arch. Wisk. 5, 372-379, 2000.

Bondareva, I. V.; Luchin, M. Y.; and Salikhov, V. K. "Symmetrized Polynomials in a Problem of Estimating the Irrationality Measure of the Number 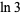." Chebyshevskiĭ Sb. 19, 15-25, 2018.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 3-4, 2004.

Borwein, J. M. and Borwein, P. B. "Irrationality Measures." §11.3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 362-386, 1987.

Finch, S. R. "Liouville-Roth Constants." §2.22 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 171-174, 2003.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford: Clarendon Press, 1979.

Hata, M. "Legendre Type Polynomials and Irrationality Measures." J. reine angew. Math. 407, 99-125, 1990.

Hata, M. "Improvement in the Irrationality Measures of 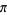 and 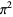." Proc. Japan. Acad. Ser. A Math. Sci. 68, 283-286, 1992.

Hata, M. "Rational Approximations to 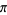 and Some Other Numbers." Acta Arith. 63, 335-349, 1993.

Hata, M. "A Note on Beuker's Integral." J. Austral. Math. Soc. 58, 143-153, 1995.

Hata, M. "A New Irrationality Measure for 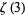." Acta Arith. 92, 47-57, 2000.

Marcovecchio, R. "The Rhin-Viola Method for 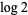." Acta Arith. 139, 147-184, 2009.

Matala-Aho, T.; Väänänen, K.; abd Zudilin, W. "New Irrationality Measures for 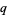-Logarithms." Math. Comput. 75, 879-889, 2006.

Rhin, G. and Viola, C. "On a Permutation Group Related to 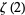." Acta Arith. 77, 23-56, 1996.

Rhin, G. and Viola, C. "The Group Structure for 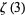." Acta Arith. 97, 269-293, 2001.

Rukhadze, E. A. "A Lower Bound for the Rational Approximation of 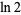 by Rational Numbers." [In Russian]. Vestnik Moskov Univ. Ser. I Math. Mekh., No. 6, 25-29 and 97, 1987.

Salikhov, V. Kh. "On the Irrationality Measure of 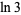."Dokl. Akad. Nauk 417, 753-755, 2007. Translation in Dokl. Math. 76, No. 3, 955-957, 2007.

Salikhov, V. Kh. "On the Irrationality Measure of 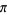." Usp. Mat. Nauk 63, 163-164, 2008. English transl. in Russ. Math. Surv 63, 570-572, 2008.

Sondow, J. "Irrationality Measures, Irrationality Bases, and a Theorem of Jarnik." Proceedings of Journées Arithmétiques, Graz 2003 in the Journal du Theorie des Nombres Bordeaux. http://arxiv.org/abs/math.NT/0406300.

Stark, H. M. An Introduction to Number Theory. Cambridge, MA: MIT Press, 1994.

van Assche, W. "Little 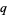-Legendre Polynomials and Irrationality of Certain Lambert Series." Jan. 23, 2001. http://wis.kuleuven.be/analyse/walter/qLegend.pdf.

Zeilberger, D. and Zudilin, W. "The Irrationality Measure of 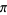 is at Most 7.103205334137...." 8 Jan 2020. https://arxiv.org/abs/1912.06345.

Zudilin, V. V. "An Essay on the Irrationality Measures of 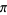 and Other Logarithms." Chebyshevskiĭ Sb. 5, 49-65, 2004.

Zudilin, V. V. "On the Irrationality Measure of 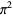." Russian Math. Surveys 68, 1133-1135, 2013.