


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-5-2020
Date: 30-12-2020
Date: 26-7-2020
|

The answer to the question "which fits better, a round peg in a square hole, or a square peg in a round hole?" can be interpreted as asking which is larger, the ratio of the area of a circle to its circumscribed square, or the area of the square to its circumscribed circle? In two dimensions, the ratios are  and
and  , respectively. Therefore, a round peg fits better into a square hole than a square peg fits into a round hole (Wells 1986, p. 74).
, respectively. Therefore, a round peg fits better into a square hole than a square peg fits into a round hole (Wells 1986, p. 74).
However, this result is true only in dimensions 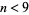 , and for
, and for 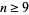 , the unit
, the unit  -hypercube fits more closely into the
-hypercube fits more closely into the 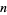 -hypersphere than vice versa (Singmaster 1964; Wells 1986, p. 74). This can be demonstrated by noting that the formulas for the content
-hypersphere than vice versa (Singmaster 1964; Wells 1986, p. 74). This can be demonstrated by noting that the formulas for the content 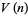 of the unit
of the unit 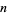 -ball, the content
-ball, the content 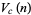 of its circumscribed hypercube, and the content
of its circumscribed hypercube, and the content 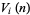 of its inscribed hypercube are given by
of its inscribed hypercube are given by
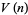 |
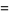 |
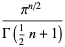 |
(1) |
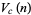 |
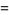 |
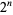 |
(2) |
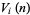 |
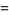 |
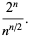 |
(3) |
The ratios in question are then
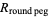 |
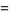 |
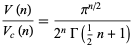 |
(4) |
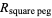 |
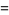 |
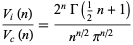 |
(5) |
(Singmaster 1964). The ratio of these ratios is the transcendental equation
![(R_(round peg))/(R_(square peg))=(pi^nn^(n/2))/(2^(2n)[Gamma(1+1/2n)]^2),](https://mathworld.wolfram.com/images/equations/Peg/NumberedEquation1.gif) |
(6) |
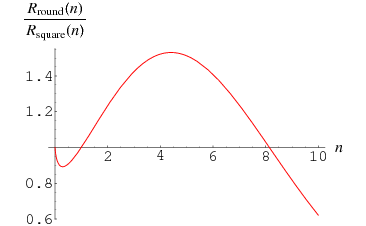
illustrated above, where the dimension 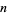 has been treated as a continuous quantity. This ratio crosses 1 at the value
has been treated as a continuous quantity. This ratio crosses 1 at the value 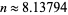 (OEIS A127454), which must be determined numerically. As a result, a round peg fits better into a square hole than a square peg fits into a round hole only for integer dimensions
(OEIS A127454), which must be determined numerically. As a result, a round peg fits better into a square hole than a square peg fits into a round hole only for integer dimensions 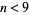 .
.
REFERENCES:
Singmaster, D. "On Round Pegs in Square Holes and Square Pegs in Round Holes." Math. Mag. 37, 335-339, 1964.
Sloane, N. J. A. Sequence A127454 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 74, 1986.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|