Laplace Limit

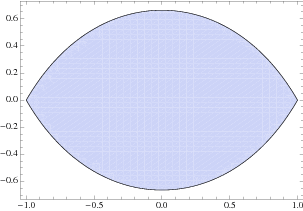
Let 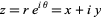 be a complex number, then inequality

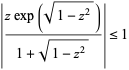(1)

holds in the lens-shaped region illustrated above. Written explicitly in terms of real variables, this can be written as

(2)

where

(3)

The area enclosed is roughly

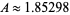(4)

(OEIS A140133).

This region can be parameterized in terms of a variable 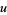 as

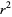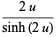			(5)
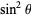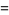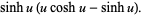			(6)

Written parametrically in terms of the Cartesian coordinates,

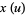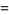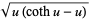			(7)
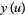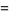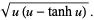			(8)

This region is intimately related to the study of Bessel functions and Kapteyn series (Plummer 1960, p. 47; Watson 1966, p. 270).

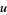 reaches its maximum value at  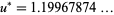(OEIS A085984; Goursat 1959, p. 120; Le Lionnais 1983, p. 36), given by the root of

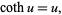(9)

or equivalently by the root of

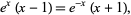(10)

as noted by Stieltjes.

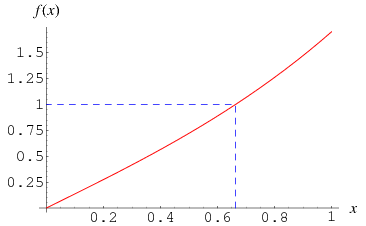
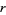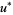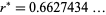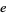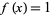The minimum value of  corresponding to the maximum value  is  (OEIS A033259; Plummer 1960, p. 47; Watson 1966, p. 270), which is known as the Laplace limit constant. It is precisely the point at which Laplace's formula for solving Kepler's equation begins diverging, and is given by the unique real solution  of  for

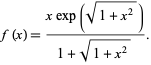(11)

The continued fraction of 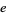 is given by [0, 1, 1, 1, 27, 1, 1, 1, 8, 2, 154, ...] (OEIS A033260). The positions of the first occurrences of  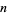in the continued fraction of  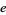are 2, 10, 35, 13, 15, 32, 101, 9, ... (OEIS A033261). The incrementally largest terms in the continued fraction are 1, 27, 154, 1601, 2135, ... (OEIS A033262), which occur at positions 2, 5, 11, 19, 1801, ... (OEIS A033263).

REFERENCES:

Finch, S. R. "Laplace Limit Constant." §4.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 266-268, 2003.

Goursat, E. A Course in Mathematical Analysis, Vol. 2: Functions of a Complex Variable & Differential Equations. New York: Dover, p. 120, 1959.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 36, 1983.

Plummer, H. An Introductory Treatise of Dynamical Astronomy. New York: Dover, 1960.

Sloane, N. J. A. Sequences A033259, A033260, A033261, A033262, A033263, A085984, and A140133 in "The On-Line Encyclopedia of Integer Sequences."

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.